Как определить объем комнаты: Страница не найдена — Тепло Проект

Периметр, площадь и объем

Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.

Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ.

perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P

= 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

Умножим длину (4 м) на ширину (3 м).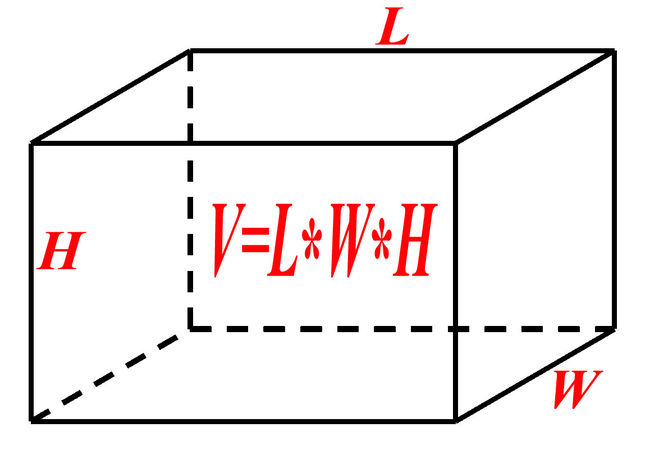

4 × 3 = 12

Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза

«квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

3 × 3 = 9

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 3

2.

Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.

Обозначения

Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной

a см будет вычисляться по следующему правилу

S = a2

где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.

Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см

2. Это обозначение заменяет словосочетание «квадратный сантиметр».

Например, вычислим площадь квадрат со стороной 2 см.

Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:

Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».

Вычислим площадь квадрата со стороной 3 метра

Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:

Аналогичные обозначения используются при вычислении площади прямоугольника.

Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

S = a × b

Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.

Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см

Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:

В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).

Перевод единиц измерения площади

Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.

1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.

Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см

Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100

S = 1002 = 10 000 см2

Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.

1 м2  = 10 000 см2

Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.

Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.

А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.

Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»

100 000 см2 : 10 000 см2 = 10 м2

Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.

Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000

S = 10002 = 1 000 000 м2

Получается, что на один квадратный километр приходится один миллион квадратных метров:

1 км2  = 1 000 000 м2

Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.

Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.

Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000

2 км2 × 1 000 000 = 2 000 000 м2

А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.

Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»

3 500 000 м2 : 1 000 000 м2 = 3,5 км2

Пример 2. Выразить 7 м2 в квадратных сантиметрах.

Умножим 7 м2 на 10 000

7 м2 = 7 м2 × 10 000 = 70 000 см2

Пример 3.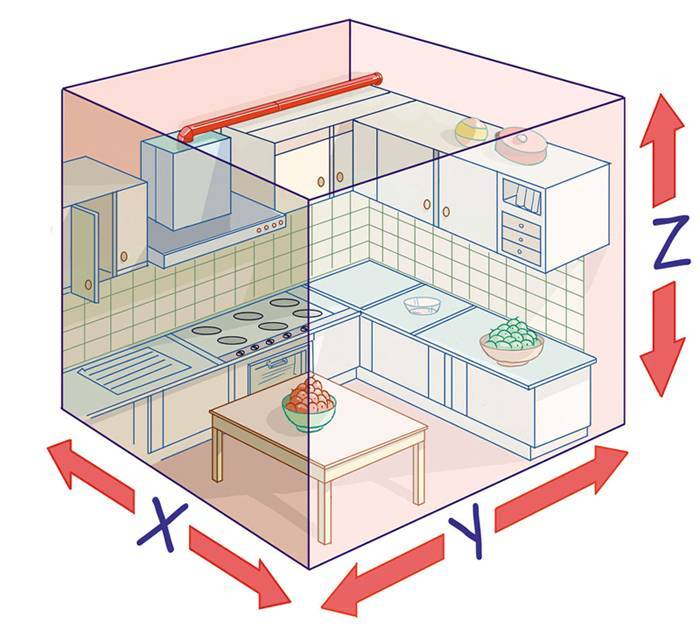 Выразить 5 м2 13 см2 в квадратных сантиметрах.

5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2

Пример 4. Выразить 550 000 см2 в квадратных метрах.

Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2

550 000 см2 : 10 000 см2 = 55 м2

Пример 5. Выразить 7 км2 в квадратных метрах.

Умножим 7 км2 на 1 000 000

7 км2 × 1 000 000 = 7 000 000 м2

Пример 6. Выразить 8 500 000 м2 в квадратных километрах.

Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2

8 500 000 м2 × 1 000 000 м2 = 8,5 км2

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:

3 а = 100 м2 × 3 = 300 м2

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:

1 сотка = 100 м2

2 сотки = 200 м2

10 соток = 1000 м2

Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:

20 га = 10 000 м2 × 20 = 200 000 м2

Прямоугольный параллелепипед и куб

Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

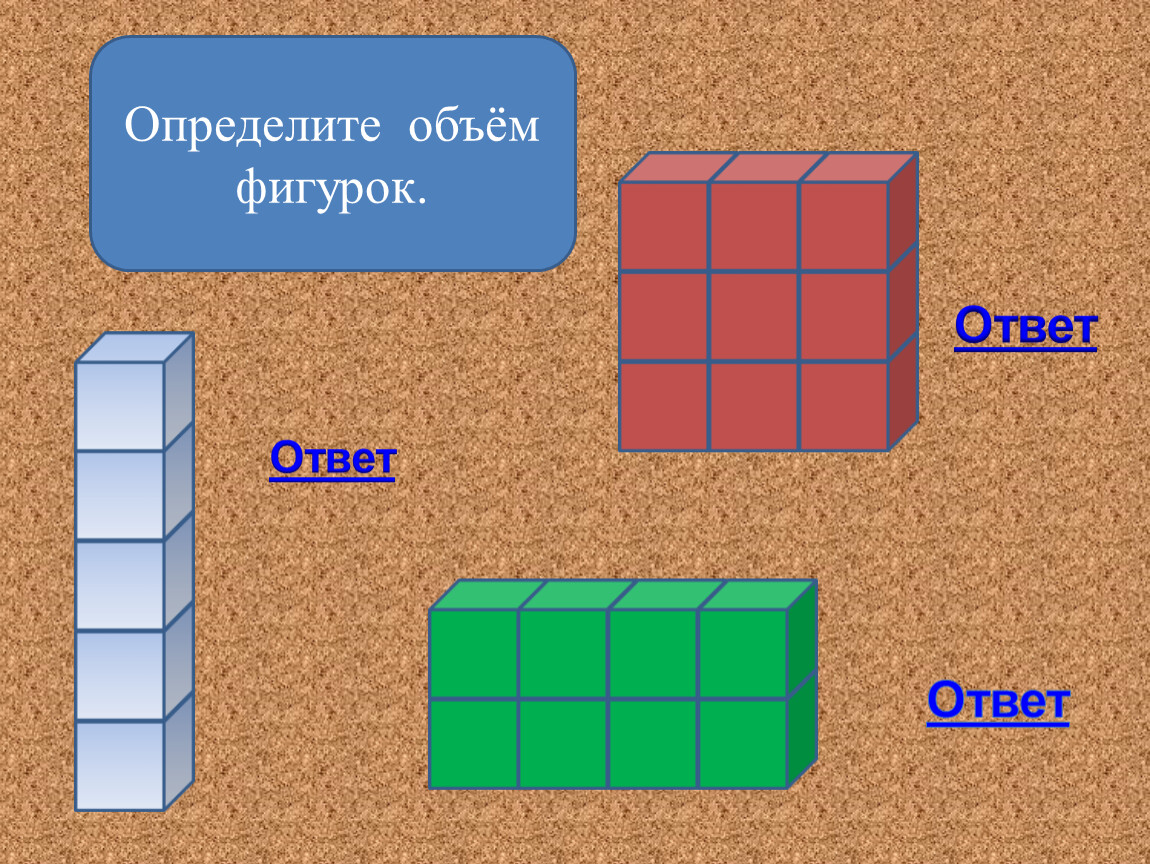
Объём геометрической фигуры

Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.

Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.

Измерить объём какой-нибудь фигуры означает выяснить сколько  кубических единиц вмещается в данную фигуру.

Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:

Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:

Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3

V = 12 см3

Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .

Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

V = abc

где, a — длина, b — ширина, c — высота

Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат

Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.

Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:

Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:

V = 3 × 3 × 3 = 27 см³

Действительно, в исходный куб вмещается 27 кубиков длиной 1 см

При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.

V = 33 = 27 см3

Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.

Таким образом, объём куба вычисляется по следующему правилу:

V = a3

Где a — длина куба.

Кубический дециметр. Кубический метр

Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).

Другое название одного кубического дециметра – один литр.

1 дм3 = 1 литр

Перевод единиц измерения объёма

Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:

Пример 1. Выразить 1 кубический метр в кубических сантиметрах.

Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.

Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см

Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:

V = 1003 = 1 000 000 см3

Получается, что на один кубический метр приходится один миллион кубических сантиметров:

1 м3  = 1 000 000 см3

Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.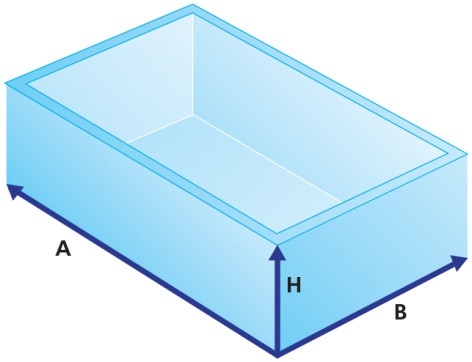

Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.

А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.

Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»

300 000 000 см3 : 1 000 000 см3 = 300 м3

Пример 2. Выразить 3 м3 в кубических сантиметрах.

Умножим 3 м3 на 1 000 000

3 м3 × 1 000 000 = 3 000 000 см3

Пример 3. Выразить 60 000 000 см3 в кубических метрах.

Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3

60 000 000 см3 : 1 000 000 см3 = 60 м3

Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.

1 литр = 1 дм3

Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.

Пример 1. Перевести 5 литров в кубические дециметры.

Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1

5 л × 1 = 5 дм3

Пример 2. Перевести 6000 литров в кубические метры.

Шесть тысяч литров это шесть тысяч кубических дециметров:

6000 л × 1 = 6000 дм3

Теперь переведём эти 6000 дм3 в кубические метры.

Длина, ширина и высота одного кубического метра равны 10 дм

Если вычислить объём этого куба в дециметрах, то получим 1000 дм3

V = 103= 1000 дм3

Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3

6 000 дм3 : 1 000 дм3 = 6 м3

Значит, 6000 л = 6 м3.

Таблица квадратов

В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.

Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.

Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.

Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.

Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576

242 = 576

Таблица кубов

Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.

Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.

353 = 42875

Задания для самостоятельного решения

Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.

Решение

P = 2(a + b)

a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см

Ответ: периметр прямоугольника равен 16 см.

Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.

Решение

S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2

Ответ: площадь равна 12 см2.

Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.

Решение

S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2

Ответ: ширина прямоугольника составляет 2 см.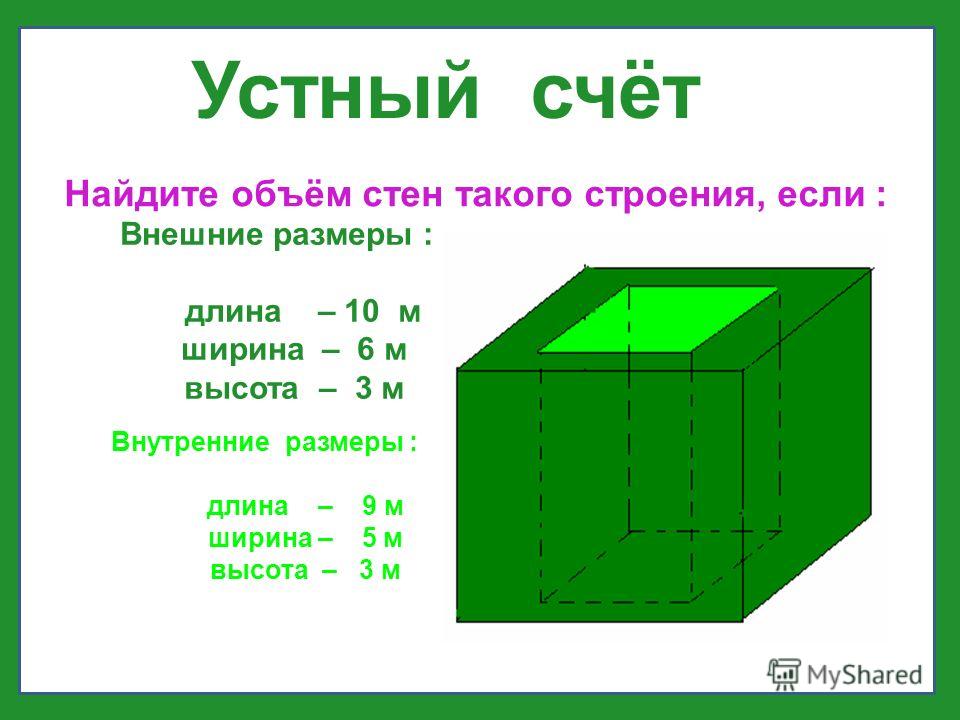

Задача 4. Вычислите площадь квадрата со стороной 8 см

Решение

S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2

Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.

Решение

V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.

Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3

Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см

Решение

V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4

Ответ: высота прямоугольного параллелепипеда равна 4 см.

Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га

Решение

Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.

Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.

Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза

4 × 3 = 12 га

Ответ: пшеницей засеяно 12 га.

Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.

Решение

a — длина
b — ширина
c — высота

a = 42 м
b = м
c = 42 × 0,1 = 4,2 м

Определим объем зернохранилища:

V = abc = 42 × 30 × 4,2 = 5292 м3

Определите сколько тонн зерна вмещает зернохранилище:

5292 × 740 = 3916080 кг

Переведём килограммы в тонны:

Ответ: зернохранилище вмещает 3916,08 тонн зерна.

Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.

Решение

Определим сколько литров в минуту вливается через вторую трубу:

25 л/мин × 0,75 = 18,75 л/мин

Определим сколько литров в минуту вливается в бассейн через обе трубы:

25 л/мин + 18,75 л/мин = 43,75 л/мин

Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин

43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л

1 л = 1 дм3

35 525 л = 35 525 дм3

Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:

35 525 дм3 : 1000 дм3 = 35,525 м3

Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:

V = 35,525
a = 5.8
b = 3.5
c = x

35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м

с = 1,75

Ответ: высота (глубина) бассейна составляет 1,75 м.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Объем комнаты и площадь пола

Вот такая вот интересная задачка:

Объем комнаты 75 метров кубических, высота комнаты 3 метра. Найдите площадь пола.

Решение задачи тупо:

75 : 3 = 25 (метров квадратных)

Если объем комнаты разделить на её высоту, то получится площадь пола. Если в вашей задаче написано «объем комнаты 75 метров квадратных…», то значит эту задачу составляло туловище, которое ни фига не понимает в единицах измерения объемов. Объем не может измеряться в метрах квадратных, нормальные люди в них измеряют площадь.

А теперь бла-бла-бла на заданную тему.

Ничего сложного в этой задаче нет, просто вместо обычного прямоугольного параллелепипеда здесь нам рассказывают о комнате. В переводе на язык математики и применительно к параллелепипеду эта задача будет звучать так:

Объем прямоугольного параллелепипеда равен 75 кубических метров, его высота равна 3 метра. Найдите площадь основания этого прямоугольного параллелепипеда.

В чём маленький подвох, который многих может сбить с толку? Дело в том, что комнату мы  привыкли видеть изнутри.

Высота комнаты и площадь пола
Эта комната изображена на стадии ремонта. После ремонта можете обставить её мебелью по своему вкусу. Кстати, большинство людей вспоминают про геометрию именно после начала ремонта — площади, периметры, объемы… Так вот, математики нам показывают прямоугольные параллелепипеды всегда снаружи.
Прямоугольный параллелепипед с обозначениями
Если в математике мы привыкли видеть любой объем снаружи, то попадая внутрь реального объема очень легко растеряться.

Теперь разберемся с названиями. То, что в комнате называется «объем комнаты», в математике называется просто «объем». «Высота комнаты» в математике будет просто «высота», а «площадь пола» — это ничто иное, как «площадь основания». Хорошо или плохо, но математики нас учат, что если площадь основания умножить на высоту, то мы получим объем. При решении задачи мы объем разделили на высоту и получили площадь.

Еще один интересный момент. Комната может иметь любую форму с вертикальными стенами. Пол в комнате может быть квадратным, прямоугольным, треугольным, шестиугольным, круглым, бесформенным. .. В любом случае, его площадь будет равна 25 квадратных метров. Ведь любая двухмерная геометрическая фигура может иметь площадь в 25 метров в квадрате. При умножении этой площади на высоту в 3 метра мы всегда будем получать объем в 75 метров кубических.

Является ли подобная задача реальной? Волне. В отдельных бюрократических документах можно встреть объем комнаты. Например, при установке газового оборудования требования могут предъявляться не к площади комнаты, а к её объему. Исходя из высоты комнаты, которая может быть разной в разных зданиях, определяют требуемую площадь пола для соблюдения строительных норм. Фокус в том, что в горении принимает участие газ кислород и его должно быть необходимое количество. Нужный объем кислорода может находиться как в маленькой и высокой комнате, так и в большой, но низкой. Разные числа при умножении могут давать один и тот же результат.

P.S. Кстати, на сайте «Русский текст» вы можете найти редкие и уникальные тексты, статьи из старых газет, интересные публикации на русском языке. Любознательность ещё никому не навредила. Конечно, если любознательностью попользоваться с умом. Если вы прочтете какую-нибудь старую, давно забытую, но интересную статью о науке — вы станете умнее, чем были до этого.

методы расчета и формулы, примеры и объём помещения по формуле, сложные фигуры


Зачем это нужно

При выполнении ремонта или строительных работ возникает необходимость узнать площадь стен, пола и потолка. Эта информация позволит планировать то, сколько строительных материалов потребуется для проведения работы.

Например, если нужно поклеить обои или провести покраску стен, то точное знание их площади поможет узнать, сколько необходимо закупать обоев или краски. Если планируется сделать навесной потолок, то без знания его площади нельзя будет правильно запланировать проведение работ. Площадь пола потребуется при работах, связанных с установкой нового покрытия или в случае, если хозяин планирует сделать тёплый пол.

Нормы расходов строительных материалов можно узнать в интернете, или в строительных магазинах. Зная эти показатели и площадь поверхности, можно посчитать стоимость проведения работ.


Подсчет квадратуры очень важен при планировании ремонтных работ Источник sense-life.com

Смотрите также: Популярные проекты дачных домов площадью до 50 кв.м.

Прямоугольный параллелепипед и куб

Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:

Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.

Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:

Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

  1. Калькулятор для проведения вычислений.
  2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров.
  3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей.
  4. Также потребуется бумага и карандаш для ведения записей в процессе работы.

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон.


Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрии Источник stroychik.ru

Смотрите также: Компании, специализирующиеся на садовых домиках и ландшафтном дизайне.

При этом важно учитывать следующее.

  • Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение.
  • Вычисления позволяют получить нужные цифры с высокой точностью. Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило.

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.


Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычислений Источник www.buvbaze.lv

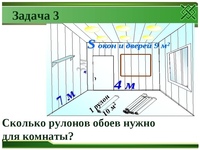
Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

  • Определяется площадь стены без учёта двери или окна.
  • Вычисляется площадь каждого окна или двери путём умножения их длины на ширину.
  • Из площади стены вычитают площадь окон и дверей.

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Объем комнаты

Формула расчета объема комнаты

Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:

  • длинна — 5,6 м;
  • ширина — 3,2 м;
  • высота — 2,5 м.

Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.

Несколько советов

  • Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем.
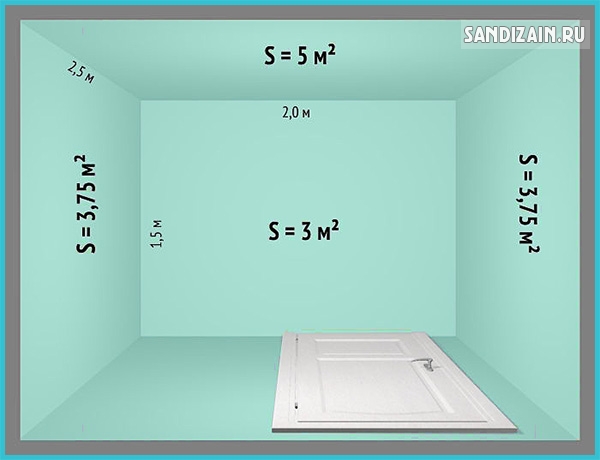
  • При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта.

Что такое жилое помещение

Перед тем как делать расчет площади дома по стенам, необходимо уточнить несколько нюансов. Во-первых, нужно знать определение жилого дома. Во-вторых, необходимо определить, что подразумевается под жилыми помещениями.

Итак, согласно законодательству, жилой дом – это отдельно стоящее строение, в котором проживает одна семья. В него входят жилые и другие помещения, предназначенные для комфортного проживания. Жилыми считаются все отапливаемые помещения. Неотапливаемые помещения, такие как балконы, не являются жилыми.

Когда осуществляется расчет площади жилого дома, учитываются площади всех жилых (гостиные, спальни, кабинеты и так далее) и вспомогательных (кухня, туалет, ванная комната, санузел, котельная и так далее) помещений.

Коротко о главном

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их.

Оценок 0

Прочитать позже

Периметр геометрической фигуры

Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:

Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.

У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:

Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:

P = 9 см + 4 см + 9 см + 4 см = 26 см.

Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»

P = 2 × (9 + 4) = 18 + 8 = 26 см.

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»

Чтобы вычислить периметр, сложим все стороны:

P = 5 см + 5 см + 5 см + 5 см = 20 см

Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения.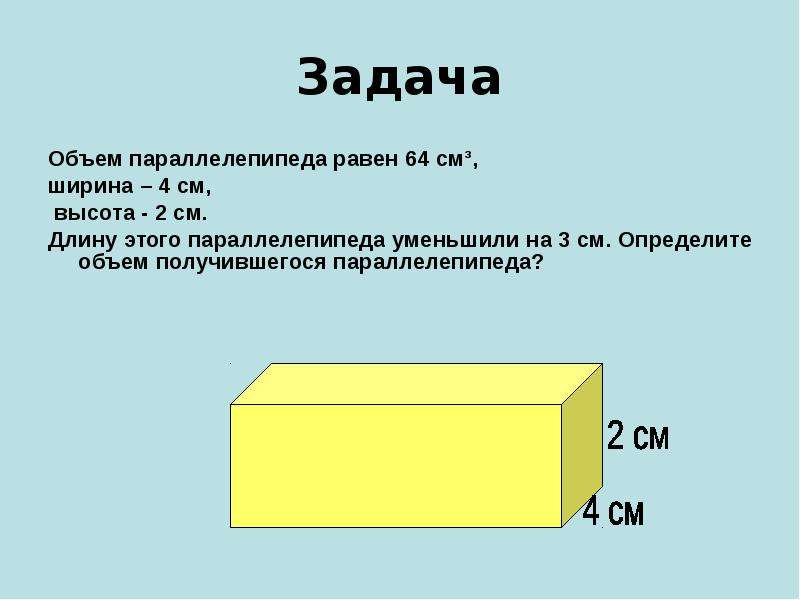 Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза

P = 5 см × 4 = 20 см

Виды треугольников

Треугольник представляет собой многоугольник, который имеет три стороны и может быть отнесен к следующим типам:

  • Равносторонний треугольник имеет равные стороны и равные углы.
  • Равнобедренный треугольник имеет две равные стороны и два равных угла.
  • Разносторонний треугольник имеет три неравные стороны и три неравных угла.
  • Прямоугольный треугольник имеет один прямой угол 90 градусов.
  • Остроугольный треугольник имеет все углы меньше 90 градусов.
  • Тупоугольный треугольник имеет один угол больше 90 градусов.

Площадь любого треугольника определяется по формулам.

1. Как рассчитать площадь треугольника, если известны высота и основание треугольника:

  • S=1⁄2×a×h, где: h – высота, a — основание.
  • S=1⁄2xa×b×sinα, где: a, b – любые две стороны, α — угол между ними.
  • S=p×r, где: p = (a+b+c) / 2 — полупериметр, a, b, c – три стороны, r – радиус круга.

Площадь равностороннего треугольника:

  • S=a2х√3 ⁄4 , где a=b= c.

Площадь равнобедренного треугольника:

2. Как рассчитать площадь треугольника, если заданы две стороны и угол между ними:

  • S=1⁄2xaxbxsinC=1⁄2xbxcxsinA =1⁄2xaxcxsinB.

Пример 1: Найти S треугольника, сторона которого составляет 14 см, а высота — 10 см.

Решение: b=14 см, h=10 см, A=1⁄2х14х10=70

Ответ: 70 см2.

Пример 2. Найти область треугольника, стороны которого и угол между ними заданы следующим образом: a=5 см и b=7 см, C=45 градусов.

Решение: Площадь треугольника =1⁄2xaxbxsin 45.

Площадь =1⁄2×5×7×0,707 (поскольку sin45=0,707)

Площадь =1⁄2×24,745=12,3725

Ответ: 12,3725 см2.

Пример 3. Найдите площадь (в м2) равнобедренного треугольника, стороны которого составляют 10 м, а основание — 12 м.

Решение: Площадь равнобедренного треугольника определяется:

A=1⁄4xbx√(4a2-b2)A=1⁄4х12х√(4х(10)2-(12)2)А=48

Ответ: 48 м2.

Пример 4. Найти площадь треугольника, стороны которого равны 8, 9 и 11 соответственно. Все единицы измерения даны в метрах (м).

Решение: Стороны a=8, b=9 и c=11. Согласно формуле Херона площадь треугольника может быть определена по следующей формуле: A=√(sx(sa)х(sb)х(sc)). Прежде всего нам нужно определить s, которая является полупериметром треугольника: s =1⁄2х(a+b+c)=1⁄2х(8+9+11)=14.

Теперь, вставив значение полупериметра в формулу Герона, можно определить площадь треугольника: A=√(sx(sa)х(sb)х(sc)). A=√(14х(14-8)х(14-9)х(14-11)). A=√(1260)=35,50

Ответ: 35,50 м2.

Формулы параллелограмма

Параллелограмм является четырехсторонним многоугольником с двумя парами параллельных сторон одинаковой длины. По определению, прямоугольник также представляет собой тип параллелограмма, но с равными углами. Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных сторон, а расстояние между сторонами.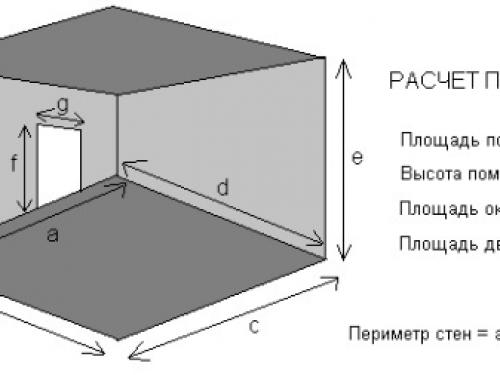

Из рисунка видно, что высота — это расстояние между двумя параллельными сторонами параллелограмма, расположенная под прямым углом между ними. S=ADxh. S=bxh, где AD=b — основание, h — высота.

Пример. Если параллелограмм имеет основание 3 см, а высоту 2 см, то площадь S равна произведению основания на высоту. Следовательно, имеем: S=3х2=6.

Ответ: 6 см2.

Измерение площади ромба

Ромб — особый вид параллелограмма, имеющий равные стороны и равные противоположные углы. Площадь ромба можно определить, используя три способа.

1. Метод высоты основания. Сначала выберите одну любую сторону в качестве базы, так как они имеют одинаковую длину. Затем определите высоту — перпендикулярное расстояние от выбранного основания до противоположной стороны.

  • Площадь является произведением этих двух величин и определяется по формуле: S=a×h, где: S – площадь ромба, h — высота ромба, AB=BC=AD=DC=a – сторона ромба.

2. Метод диагоналей. Другая простая формула для площади ромба, когда известны длины диагоналей.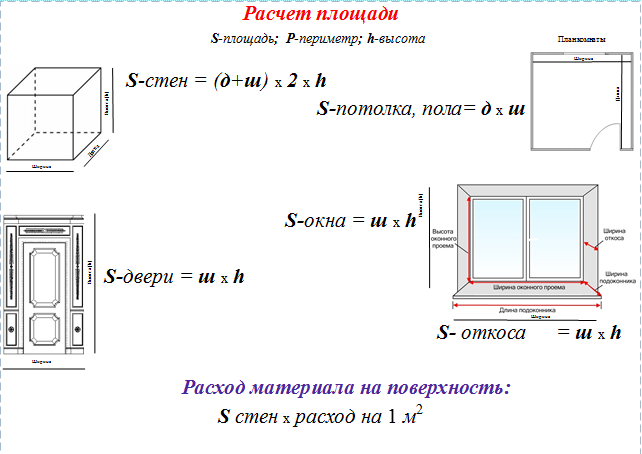 Площадь составляет половину произведения диагоналей.

  • В качестве формулы: S=1/2xACxBD, где: S – площадь ромба, AC– большая диагональ, BD — меньшая диагональ.

3. Использование тригонометрии. В тригонометрии, есть удобная формула, когда известны длина стороны и любой угол:

  • S=a2×sin α, где: S – площадь ромба, B=BC=AD=DC= a – сторона ромба, α — острый угол, β — тупой угол.

Калькулятор объема

Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».

Калькулятор объема сферы


Калькулятор объема конуса


Калькулятор объема куба


Калькулятор объема цилиндра


Калькулятор объема прямоугольного резервуара


Калькулятор объема капсулы


Калькулятор объема сферической крышки

Укажите любые два значения ниже для расчета.


Калькулятор объема усеченного конуса


Калькулятор объема эллипсоида


Калькулятор объема квадратной пирамиды


Калькулятор объема пробирки


Калькулятор площади поверхности | Калькулятор площади

Объем – это количественная оценка трехмерного пространства, занимаемого веществом.Единицей объема в СИ является кубический метр, или м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.

Сфера

Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, равноудаленных от заданной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r . Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема сферы приведено ниже:

EX: Клэр хочет наполнить идеально сферический шарик с водой радиусом 0.15 футов с уксусом, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные. Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:

объем = 4/3 × π × 0,15 3 = 0,141 фута 3

Конус

Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание).На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:

где r радиус и h высота конуса

EX: Беа полна решимости выйти из магазина мороженого с хорошо потраченными с трудом заработанными 5 долларами. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее.Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:

объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйма 3

Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.

Куб

Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим смежным граням. Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр.Ниже приведено уравнение для расчета объема куба:

объем = 3
где a — длина ребра куба

ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, не похожей ни на что другое, с чем он когда-либо сталкивался, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть кубический чемодан с длиной ребра 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:

объем = 2 3 = 8 футов 3

Цилиндр

Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси.Однако в обычном употреблении «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . . Уравнение для расчета объема цилиндра показано ниже:

объем = πr 2 ч
где r радиус и h высота бака

EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он решительно выступает за переработку отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:

объем = π × 3 2 × 4 = 113,097 футов 3

Он успешно строит замок из песка в своем доме и, в качестве дополнительного бонуса, ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.

Прямоугольный бак

Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:

объем = длина × ширина × высота

EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам.Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:

.

объем = 2 × 3 × 4 = 24 фута 3

Капсула

Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы.Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:

объем = πr 2 ч + πr 3 = πr 2 ( р + ч)

где r — радиус, а h — высота цилиндрической части

EX: Учитывая капсулу радиусом 1,5 фута и высотой 3 фута, определите объем m&m’s из расплавленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет закопать для будущих поколений в своем путешествии самопознания через Гималаи:

объем = π × 1. 5 2 × 3 + 4/3 ×π ×1,5 3 = 35,343 фута 3

Сферическая крышка

Сферический колпак представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера разделена на две параллельные плоскости и два разных радиуса, где плоскости проходят через сферу. Уравнение для расчета объема сферического колпака выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, показанной в калькуляторе:

Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:

Даны r и R : h = R ± √R 2 — r 2

Даны R и h : r = √2Rh — h 2
где r — радиус основания, R — радиус сферы, а h — высота сферического колпачка

EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, он решает саботировать мяч для гольфа Джеймса. Он отрезает идеальный сферический колпачок от мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:

объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3

К несчастью для Джека, Джеймс получил новую партию мячей за день до игры, и все усилия Джека оказались напрасными.

Усеченный конус

Коническая усеченная часть — это часть твердого тела, остающаяся после разрезания конуса двумя параллельными плоскостями. Этот калькулятор вычисляет объем для прямого круглого конуса специально. Типичные усеченные конусы, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы. Объем правой конической усеченной части рассчитывается по следующему уравнению:

объем = πh(r 2 + rR + R 2 )

где r и R — радиусы оснований, h — высота усеченного конуса

EX: Беа успешно добыла немного мороженого в сахарном рожке и только что съела его таким образом, что мороженое осталось упакованным внутри рожка, а поверхность мороженого параллельна плоскости отверстия рожка.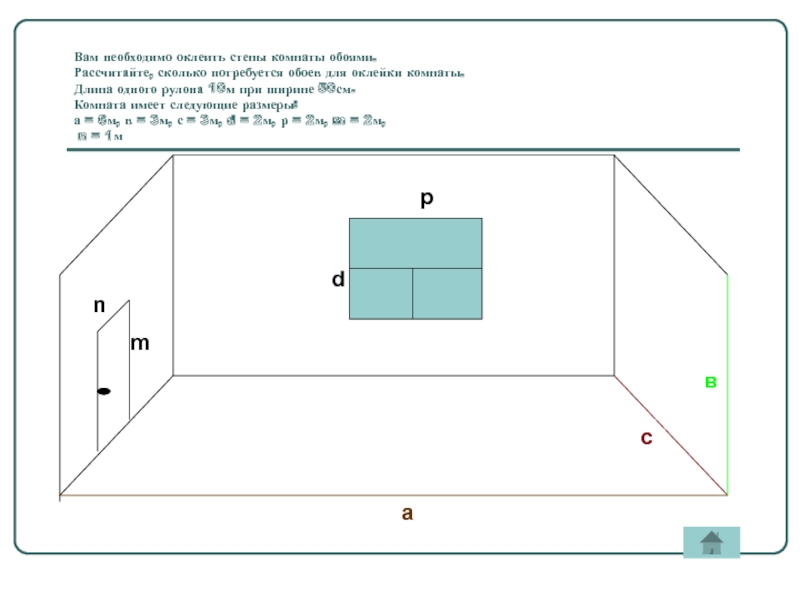 Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с правым коническим усеченным мороженым, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:

объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 в 3

Эллипсоид

Эллипсоид — это трехмерный аналог эллипса и поверхность, которую можно описать как деформацию сферы путем масштабирования направленных элементов. Центром эллипсоида называется точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:

где a , b и c длины осей

EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и разрешает ему есть столько мяса, сколько он может поместиться в булочке в форме эллипсоида. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:

объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3

Квадратная пирамида

Пирамида в геометрии — это трехмерное тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это фигура на плоскости, ограниченная конечным числом прямых отрезков. Существует множество возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — квадрат. Другое различие, связанное с пирамидами, связано с расположением вершины. Вершина правильной пирамиды находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:

Обобщенный объем пирамиды:

где b площадь основания и h высота

Объем квадратной пирамиды:

где а длина ребра основания

EX: Ван очарован древним Египтом и особенно любит все, что связано с пирамидами. Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:

объем = 1/3 × 5 2 × 12 = 100 футов 3

Трубчатая пирамида

Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газов.Вычисление объема трубы по существу использует ту же формулу, что и для цилиндра ( объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина используется, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:

где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубы

EX: Beulah занимается защитой окружающей среды.Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу, через ручей. Он хочет более легкого доступа к своему дому и просит Беулу построить ему дорогу, обеспечив при этом свободное течение ручья, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые плотины были бы хорошей точкой для прокладки трубы через ручей. Объем запатентованного ударопрочного бетона, необходимый для строительства трубы наружным диаметром 3 фута, внутренним диаметром 2.5 футов и длину 10 футов можно рассчитать следующим образом:

объем = π × × l0 = 21,6 фута 3

Общие единицы объема

2
Unit кубометров миллилитров
Milliliter (кубический сантиметр) 0,000001 1
1
0,00001639 0,00001639 16. 39
PINT 0.000473 473
кварта 0,000946 946
л 0,001 1 000
галлонов 0,003785 3785
кубический фут 0,028317 28317
кубический двор 0.764555 764 555 764 555
1 1 000 000
1 000 000 000 10 15

Вычисление объема | SkillsYouNeed

На этой странице объясняется, как рассчитать объем твердых объектов, т.е.е. сколько бы вы могли вместить в предмет, если бы, например, наполнили его жидкостью.

Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).

Объем — это мера того, сколько места находится внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.

В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.

Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.

Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.

A Примечание по устройствам

Площадь выражается в квадратных единицах ( 2 ), потому что она измеряется в двух измерениях (т.г. длина × ширина).

Объем выражается в кубических единицах ( 3 ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают см 3 , м 3 и кубические футы.

ВНИМАНИЕ!

Объем также может быть выражен как вместимость по жидкости.

Метрическая система

В метрической системе вместимость жидкости измеряется в литрах, что прямо сравнимо с кубическим измерением, поскольку 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .

Имперская/английская система

В имперской/английской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.

Для получения дополнительной информации см. нашу страницу о системах измерения.

Основные формулы для расчета объема

Объем тел на основе прямоугольников


В то время как основная формула площади прямоугольной формы равна длине 90 516 × 90 517 ширине, основная формула объема равна длине 90 516 × 90 517 ширине 90 516 × 90 517 высоте.

То, как вы ссылаетесь на различные измерения, не влияет на вычисление: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, который вам нравится, так как это не изменит ответ (подробнее см.

Коробка с размерами 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3

Объем призм и цилиндров

Эта базовая формула может быть распространена на объем цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.

По сути, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.

Таким образом, основная формула объема призм и цилиндров:

Площадь торца × высота/глубина призмы/цилиндра.

Остерегайтесь несовместимых юнитов!

Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1 см.7м. Рассчитайте объем воды в трубе.

В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr 2 . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 2 , что составляет 3,14 см 2 .

Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.

Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.

Таким образом, объем равен 3,14 × 1700 = 5338 см 3 . Это эквивалентно 5,338 литра или 0,0053 м 3 .

Объем конусов и пирамид

Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю от общего объема, который был бы, если бы они продолжали одинаковой формы (в поперечном сечении) насквозь.

Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.

Таким образом, формула:

Площадь основания или торца × высота конуса/пирамиды × 1 / 3

Вернитесь к нашей странице Вычисление площади , если вы не можете вспомнить, как вычислить площадь круга или треугольника.

Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:

Площадь внутри круга = πr 2 (где π (пи) приблизительно равно 3.14, а r — радиус окружности).

В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .

78,5 × 10 = 785

785 × 1/3 = 261,6667 см 3

Объем сферы

Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.

Формула 4/3 × π × радиус 3 .

Вам может быть интересно, как можно вычислить радиус шара.Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.

Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.

Длина окружности рассчитывается как 2 x π x радиус.

Чтобы вычислить радиус по окружности вам:

Разделите длину окружности на (2 x π) .

Примеры работы: расчет объема

Пример 1

Вычислите объем цилиндра длиной 20 см, радиус круглого конца которого равен 2,5 см.

Сначала определите площадь одного из круглых концов цилиндра.

Площадь круга равна πr 2 (π × радиус × радиус). π (пи) примерно равно 3,14.

Таким образом, площадь конца:

3. 14 х 2,5 х 2,5 = 19,63 см 2

Объем — это площадь конца, умноженная на длину, и поэтому:

19,63 см 2 x 20 см = 392,70 см 3




Пример 2

Что больше по объему: сфера радиусом 2 см или пирамида с основанием 2,5 см и высотой 10 см?

Сначала определите объем сферы .

Объем сферы равен 4/3 × π × радиусу 3 .

Таким образом, объем сферы равен:

4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3

Затем определите объем пирамиды .

Объем пирамиды равен 1/3 × площадь основания × высота.

Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2

Таким образом, объем

равен 1/3 х 6,25 х 10 = 20.83см 3

Таким образом, сфера больше по объему, чем пирамида.


Расчет объема неправильных тел

Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных тел. Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.

Рабочий пример

Рассчитайте объем водяного цилиндра общей высотой 1 м и диаметром 40 см, верхняя часть которого имеет форму полусферы (половина сферы).

Сначала вы делите фигуру на две части: цилиндр и полусферу.

Объем сферы равен 4/3 × π × радиусу 3 . В этом примере радиус равен 20 см (половина диаметра). Поскольку вершина полусферическая, ее объем будет вдвое меньше полной сферы. Таким образом, объем этой секции формы:

0,5 × 4/3 × π × 20 3 = 16 755,16 см 3

Объем цилиндра равен площади основания × высоте. Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, который равен 1 м — 20 см = 80 см. Площадь основания πr 2 .

Таким образом, объем цилиндрического сечения этой формы:

80 × π × 20 × 20 = 100 530,96 см 3

Таким образом, общий объем этого контейнера для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .

Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000см 3 ). Однако вполне корректно выразить ее как cm 3 , так как задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.



Дополнительное чтение из навыков, которые вам нужны

Понимание геометрии
Часть руководства по необходимым навыкам счета

В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

В заключение…

Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем почти всего в вашей жизни, будь то упаковочный ящик, комната или водяной цилиндр.

Калькулятор кубических футов

(футы, дюймы, см, ярды)

Как рассчитать кубические футы

Кубический фут — это единица измерения объема .Чтобы рассчитать объем или вместимость предмета или пространства в кубических футах, вам сначала нужно измерить его длину, ширину и высоту в футах, дюймах (или в обоих), сантиметры, метры или ярды. Получив эти измерения, вы применяете умножение следующим образом…

Расчет кубических футов для различных единиц измерения (формулы)

  • С футов: длина (футы) × ширина (футы) × высота (футы) = кубические футы
  • Из дюймов: длина (дюймы) × ширина (дюймы) × высота (дюймы) ÷ 1728 = кубические футы
  • Из ярдов: длина (ярды) × ширина (ярды) × высота (ярды) × 27 = кубические футы
  • Из см: длина (см) × ширина (см) × высота (см) ÷ 28316. 85 =
    • кубических футов
  • Из метров: длина (м) × ширина (м) × высота (м) × 35,314667 = кубические футы

Давайте рассмотрим каждый из них по очереди.

Расчет кубических футов на основе измерений в футах

Если вы измерили ширину, длину и высоту вашего предмета в футах, то процесс расчета прост: просто перемножьте 3 цифры вместе.

В качестве примера предположим, что вы ищете вместимость коробки, которая размеры 5 футов на 3 фута на 2 фута.Умножение этих трех цифр дает общее значение кубических футов 30 футов 3 .

Если вы уже рассчитали свою площадь в квадратных футах, вам просто нужно умножить эту цифру на измерение высоты.

Если вы хотите измерить холодильник, взгляните на нашу статью, сколько кубических футов мой холодильник?

Реклама

Вычисление кубических футов из дюймов

Если вы измерили размеры вашего предмета в дюймах, сделайте следующее:

  1. Умножьте свои значения длины, ширины и высоты вместе, чтобы получить общую сумму в кубических дюймах (в 3 )
  2. Разделите полученную сумму на 1728 (поскольку в кубическом футе 1728 кубических дюймов).

В качестве примера предположим, что вы ищете вместимость коробки размером 55 x 30 x 15 дюймов. Умножив эти 3 цифры вместе, вы получите общее значение кубических дюймов 24 750 дюймов 90 129 3 90 130 . Чтобы преобразовать эту цифру в кубические футы мы делим это к 1728 году, что дает в общей сложности 14,323 фута 3 .

Вычисление кубических футов из сантиметров

Если вы измерили размеры вашего предмета в сантиметрах (см), сделайте следующее:

  1. Умножьте свои значения длины, ширины и высоты вместе, чтобы получить сумму в кубических сантиметрах (см 3 )
  2. Разделите полученную сумму на 28 316.85 (поскольку в кубическом футе примерно 28 316,85 кубических см).

Вычисление кубических футов из ярдов

Если вы измерили размеры вашего предмета в ярдах, сделайте следующее:

  1. Умножьте свои значения длины, ширины и высоты, чтобы получить общую сумму в кубических ярдах (ярды 3 )
  2. Умножьте сумму на 27 (поскольку в кубическом ярде 27 кубических футов).

Получив итоговую цифру, сравните ее с калькулятором в верхней части этой страницы.В качестве альтернативы, если вы сняли мерки и хотите конвертируйте их в кубические ярды, попробуйте калькулятор кубических ярдов.

Вы можете узнать больше о том, как рассчитать кубические футы в этой статье.

Реклама

Как перевести кубические дюймы в кубические футы

Один кубический фут равен 1728 кубическим дюймам. Таким образом, чтобы преобразовать кубические дюймы в кубические футы, вы должны разделить число кубических дюймов на 1728. Если вы не хотите делать это вручную, дайте мой конвертер объема. попытка.

Какой объем спальни? — Ответы на все

Каков объем спальни?

Итак, как рассчитать объем комнаты, а именно длину, ширину, высоту? Хорошая простая формула. Возьмите длину вашей комнаты, ширину вашей комнаты и высоту вашей комнаты и умножьте эти три. Это даст вам ваш кубический объем, кубический фут объема.

Как рассчитать объем?

В то время как основная формула площади прямоугольной формы — длина × ширина, основная формула объема — длина × ширина × высота.

Как рассчитать кубатуру комнаты?

Объем комнаты: Для объема в кубических футах нашего примера комнаты сверху просто умножьте ширину на длину на высоту: (10 футов x 12 футов x 8 футов = 960 кубических футов).

Как найти объем воздуха в комнате?

Рассчитайте объем воздуха, используя скорость воздухообмена и пример использования. Для расчета требуемого объема воздуха требуется объем помещения, который определяется по формуле объем помещения = длина (м) х ширина (м) х высота (м) и назначение помещения, которое указывает скорость воздухообмена (ACH ).

Как найти объем комнаты в кубических футах?

Расчет кубических футов для различных единиц измерения (формулы)

  1. Из футов: длина (футы) × ширина (футы) × высота (футы) = кубические футы.
  2. Из дюймов: длина (дюймы) × ширина (дюймы) × высота (дюймы) ÷ 1728 = кубические футы.
  3. Из ярдов: длина (ярды) × ширина (ярды) × высота (ярды) × 27 = кубические футы.

Как измерить объем воздуха?

Умножение скорости воздуха на площадь воздуховода позволяет определить объем воздуха, проходящий через точку воздуховода в единицу времени.Объемный расход обычно измеряется в кубических футах в минуту (CFM). Скорость воздуха измеряется путем измерения давления, создаваемого движением воздуха.

Каков средний объем дома?

Средний дом на одну семью в Соединенных Штатах в целом увеличился в размерах с 2000 года. Он достиг своего пика в 2467 квадратных футов в 2015 году, а к 2019 году сократился до 2301 квадратных футов.

Как рассчитать объем комнаты?

Нарисуйте комнату, в которой нужно найти объем.Включите шкафы и ниши или области неправильной формы.

  • Снимите все размеры, указанные на чертеже — длину, высоту и ширину. Используйте одни и те же единицы измерения, будь то футы, метры или дюймы, во всех измерениях.
  • Разделите чертеж на прямоугольные области, чтобы упростить расчеты.

    • Как определить размер комнаты?

    Разделите пространство на более мелкие секции. Измерьте каждую секцию отдельно и рассчитайте площадь каждой из них. Используйте калькулятор, чтобы сложить числа вместе, чтобы получить общую площадь в квадратных футах.

    Как рассчитать площадь комнаты?

    Для расчета площади помещения необходимо знать основную формулу площади. Чтобы рассчитать площадь, вы просто умножаете длину комнаты на ширину комнаты, или площадь равна длине, умноженной на ширину.

    Как рассчитать размеры комнаты?

    Измерьте длину и ширину основной части комнаты. Чтобы рассчитать площадь комнаты, используйте стандартную формулу (Длина) x (Ширина) = Площадь. Измерьте максимальную длину и ширину в самых широких точках комнаты.Это важно и поможет вам получить правильные измерения.