Как посчитать квадратные метры в треугольнике: Как найти площадь треугольника — Лайфхакер

Как найти площадь треугольника — Лайфхакер

Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

1. Умножьте сторону треугольника на высоту, проведённую к этой стороне.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a — сторона треугольника.
• h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

1. Посчитайте произведение двух известных сторон треугольника.
2. Найдите синус угла между выбранными сторонами.
3. Перемножьте полученные числа.
4. Поделите результат на два.

• S — искомая площадь треугольника.
• a и b — стороны треугольника.
• α — угол между сторонами a и b.

Сейчас читают 🔥

Зная три стороны (формула Герона)

1. Посчитайте разности полупериметра треугольника и каждой из его сторон.
2. Найдите произведение полученных чисел.
3. Умножьте результат на полупериметр.
4. Найдите корень из полученного числа.

• S — искомая площадь треугольника.
• a, b, c — стороны треугольника.
• p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

1. Найдите произведение всех сторон треугольника.
2. Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.

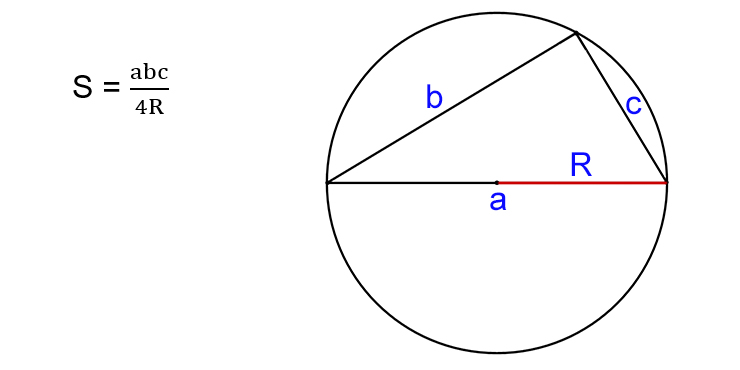
• S — искомая площадь треугольника.
• R — радиус описанной окружности.
• a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

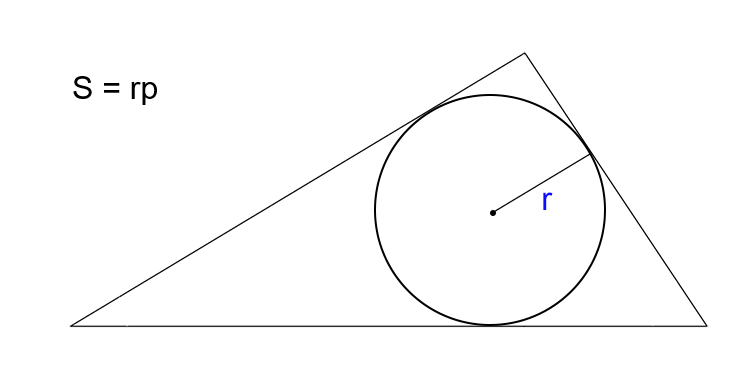
• S — искомая площадь треугольника.
• r — радиус вписанной окружности.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

1. Посчитайте произведение катетов треугольника.
2. Поделите результат на два.

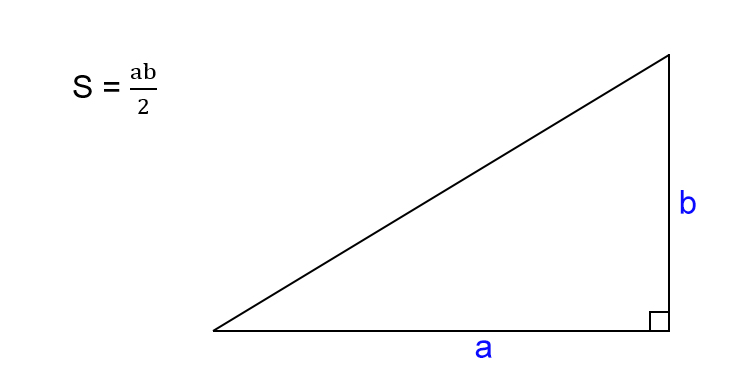
• S — искомая площадь треугольника.
• a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

1. Умножьте основание на высоту треугольника.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
• h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

1. Умножьте квадрат стороны треугольника на корень из трёх.
2. Поделите результат на четыре.

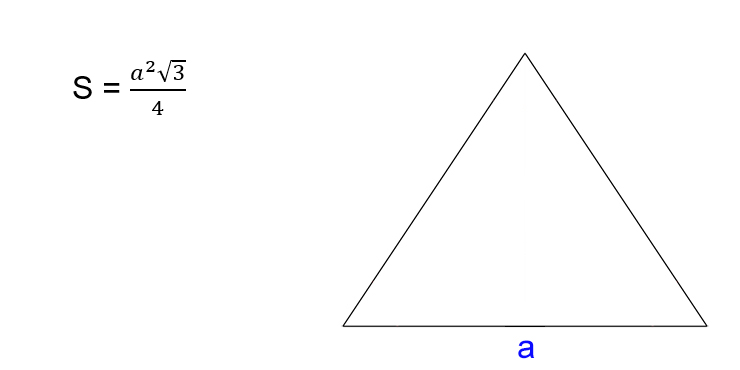
• S — искомая площадь треугольника.
• a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

Площадь треугольника

Какие размеры треугольника известны:

Основание и высота Три стороны

Результат:

Решение

Теория

  Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

  Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

По типовым особенностям формы, треугольники бывают разносторонние, прямоугольные, равнобедренные, равносторонние.

Формула площади треугольника

  Посчитать площадь треугольника можно разными способами. Это зависит от формы треугольника и известных размеров. Так есть типовые расчёты площади для прямоугольного, равнобедренного и равностороннего треугольников.

Площадь треугольника расчитывается по размерам трёх сторон по

формуле Герона или через основание и высоту треугольника.

Через основание и высоту:

S = \dfrac{1}{2} ah

• S — площадь треугольника
• h — высота
• a — основание

---

По трём сторонам через полупериметр — формула Герона:

S = \sqrt{p(p — a)(p — b)(p — c)}

p = \dfrac{a + b + c}{2}

• S — площадь треугольника
• p — полупериметр треугольника
• a, b, c — стороны треугольника

---

Похожие калькуляторы:

Площадь треугольника

Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.

Таблица с формулами площади треугольника (в конце страницы)

Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)

— Вычисления   (показано)   (скрыто)

— примечания   (показано)   (скрыто)

Для всех треугольников

---

1

Площадь треугольника по основанию и высоте

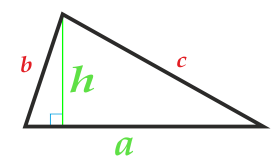
Сторона a

Высота h

Основанием треугольника может быть выбрана любая из сторон треугольника.

---

2

Площадь треугольника по двум сторонам и углу между ними

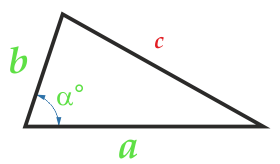
Сторона a

Сторона b

Угол α° между сторонами a и b

Угол α между сторонами может быть любым: тупым, острым, прямым.

---

3

Площадь треугольника по радиусу вписанной окружности и трем сторонам

Сторона a

Сторона b

Сторона c

Радиус r вписанной окружности

---

4

Площадь треугольника по радиусу описанной окружности и трем сторонам

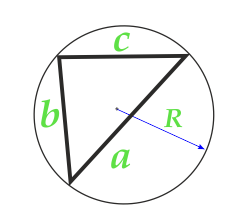
Сторона a

Сторона b

Сторона c

Радиус

R описанной окружности

---

5

Площадь треугольника по формуле Герона

Полупериметр: 

Сторона a

Сторона b

Сторона c

---

6

Площадь произвольного треугольника по стороне и двум прилежащим углам

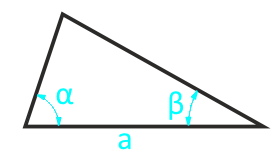
Сторона a

Угол β°

Угол α°

---

Для равнобедренных треугольников

---

7

Площадь равнобедренного треугольника по боковым сторонам и основанию

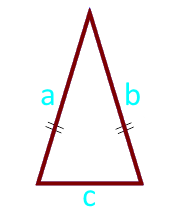
Сторона a (a = b)

Сторона c

---

8

Площадь равнобедренного треугольника по боковым сторонам и углу между ними

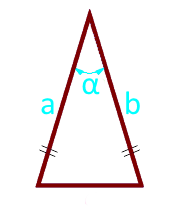
Боковая сторона a (a = b)

Угол α° между боковыми сторонами

---

9

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними

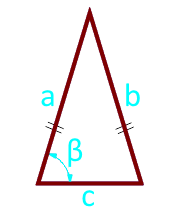
Боковая сторона a (a = b)

Основание треугольника c

Угол β° между основанием и стороной

---

10

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами

Основание треугольника c

Угол α° между боковыми сторонами

---

Для равносторонних треугольников

---

11

Площадь равнобедренного треугольника по высоте и основанию

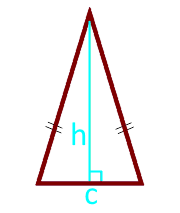
Основание треугольника c

Высота h

---

12

Площадь равностороннего треугольника по стороне

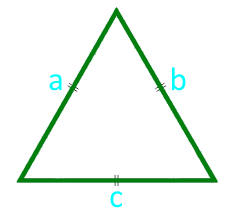
Сторона a (a = b = c)

---

13

Площадь равностороннего треугольника по высоте

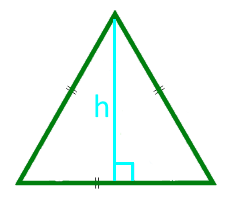
Высота h

---

14

Площадь равностороннего треугольника по радиусу вписанной окружности

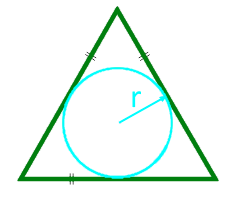
Радиус r вписанной окружности

---

15

Площадь равностороннего треугольника по радиусу описанной окружности

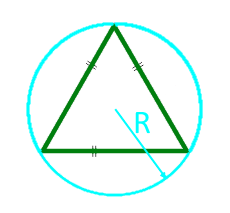
Радиус R описанной окружности

---

Для прямоугольных треугольников

---

16

Площадь прямоугольного треугольника по двум катетам

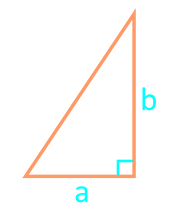
Катет a

Катет b

---

17

Площадь прямоугольного треугольника через гипотенузу и угол

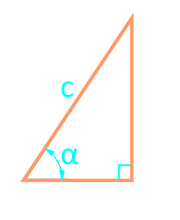
Сторона c

Угол α

---

18

Площадь прямоугольного треугольника через катет и угол

Сторона b

Угол α

---

19

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

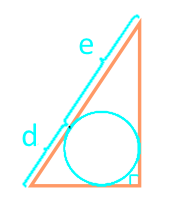
Отрезок d

Отрезок e

---

20

Площадь прямоугольного треугольника через гипотенузу и вписанную окружность

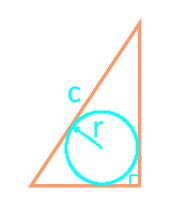
Сторона с

Радиус r

---

21

Площадь прямоугольного треугольника по формуле Герона

Полупериметр: 

Сторона a

Сторона b

Сторона c

---

Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.

Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.

---

В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.

Таблица с формулами площади треугольника

---

Определения

Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

---

Скачать формулы площади треугольника в виде картинки

Площадь треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Площадь любого треугольника можно найти, зная основание и высоту. Вся простота схемы заключается в том, что высота делит основание a на две части a₁ и a₂, а сам треугольник – на два прямоугольных треугольника, площадь которых получается и . Тогда площадь всего треугольника будет суммой двух указанных площадей, и если мы вынесем одну вторую высоты за скобку, то в сумме мы получим обратно основание:

---

Более сложный для расчетов способ – это формула Герона, для которой необходимо знать все три стороны. Для этой формулы нужно вычислить сначала полупериметр треугольника: Сама формула Герона подразумевает квадратный корень из полупериметра, умноженного поочередно на разность его с каждой из сторон.

---

Следующий способ, также актуальный для любого треугольника, позволяет найти площадь треугольника через две стороны и угол между ними. Доказательство этому проистекает из формулы с высотой – проводим высоту на любую из известных сторон и через синус угла α получаем, что h=a⋅sinα . Для вычисления площади умножим половину высоты на вторую сторону.

---

Другой способ – найти площадь треугольника, зная 2 угла и сторону между ними. Доказательство этой формулы достаточно простое, и наглядно видно из схемы.

Опускаем из вершины третьего угла высоту на известную сторону и называем полученные отрезки x соответственно. Из прямоугольных треугольников видно, что первый отрезок x равен произведению котангенса угла α на высоту, а второй отрезок y – произведению котангенса угла β на эту же высоту. Дальше соединяем это вместе:

по трем сторонам и тд

В публикации представлены онлайн-калькуляторы и формулы для расчета площади треугольника по разным исходным данным: через основание и высоту, три стороны, две стороны и угол между ними, три стороны и радиус вписанной или описанной окружности.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь треугольника.

1. Через основание и высоту

Формула расчета

2. Через длину трех сторон (формула Герона)

Примечание: если результат равен нулю, значит отрезки с указанными длинами не могут образовывать треугольник (следует из свойств треугольника).

Формула расчета:

p – полупериметр, который считается так:

3. Через две стороны и угол между ними

Примечание: максимальный угол в радианах не должен быть больше 3,141593 (приблизительное значение числа π), в градусах – до 180° (исключительно).

Формула расчета

4. Через радиус описанной окружности и стороны

Формула расчета

5. Через радиус вписанной окружности и стороны

Формула расчета

Калькулятор расчета площади треугольного помещения

Как часто домашний мастер при производстве ремонта сталкивается с необходимостью вычисления площади того или иного помещения? Никаких сложностей не возникает, если комната имеет ровные стены и форму квадрата или прямоугольника. Но что делать, если она треугольная или же все ее стены имеют различную ширину? Тогда случае поможет калькулятор расчета площади треугольного помещения. Разберемся как он работает.

Комната может быть подобной формы

Читайте в статье

Калькулятор расчета площади треугольного помещения

Как работать с онлайн-калькулятором

На самом деле все достаточно просто. Начнем с комнаты треугольной формы. В соответствующие поля программы вносим длины всех стен по очереди. На этом, собственно, вся работа заканчивается. Остается лишь нажать на кнопку «Рассчитать», после чего появится результат, выраженный в квадратных метрах.

Нюансы вычислений в комнатах с разными стенами

Здесь задача немного усложняется. Алгоритм действий разбивается на два этапа. Для начала делим комнату на 2 треугольника. После этих действий высчитываем при помощи онлайн-калькулятора параметры каждого из них и складываем. Таким же образом поступаем и с многоугольными помещениями – любое из них легко можно разбить на треугольники.

Любой многоугольник можно разбить так, чтобы можно было произвести необходимые вычисления

Конечно можно выполнить все вычисления и самостоятельно, но не факт, что провести меридианы в помещении удастся идеально ровно. А любое расхождение – это погрешность, которая совершенно не нужна в расчетах.

Если все же решено производить подобную работу самостоятельно, предлагаем просмотреть полезный видеоролик:

ПОНРАВИЛАСЬ СТАТЬЯ? Поддержите нас и поделитесь с друзьями

Калькулятор расчета площади треугольного помещения

При расчете площадей помещений или других поверхностей, подлежащих отделке, порой приходится сталкиваться с многоугольными фигурами, которые неопытного человека могут поставить в тупик. Но на самом деле – нет ничего сложного, существует простой и точный способ провести необходимые вычисления.

Калькулятор расчета площади треугольного помещения

Любой многоугольник можно одной или несколькими линиями разбить на определенное количество треугольников, затем просчитать площади этих участков и просуммировать. А чтобы вычисления были произведены быстро и точно, примените предлагаемый калькулятор расчета площади треугольного помещения.

Несколько пояснений по работе с ним будут даны ниже.

Калькулятор расчета площади треугольного помещения

Перейти к расчётам

Несколько необходимых пояснений

Треугольные помещения встречаются нечасто, но калькулятор может быть полезен и в иных случаях. Как уже говорилось, на треугольники несложно разбить любую многоугольную плоскую фигуру.

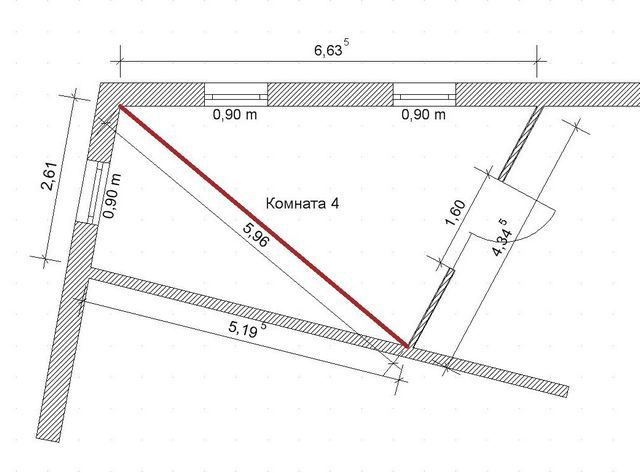Пример разбивки неправильного четырёхугольника на два треугольника

Площадь треугольника чаще определяют произведением основания на высоты с последующим делением на два. Однако, в условиях стройки или ремонта пробить перпендикуляр, чтобы точно измерить высоту фигуры – не всегда бывает просто, если нет специальных инструментов. Даже небольшая ошибка в разметке способна привести к искажению конечного результата. Поэтому в данном случае применена формула Герона, позволяющая рассчитать площадь абсолютно любого треугольника по длинам трех его сторон, измерить которые – уже труда никакого не составит.

Значения запрашиваются в сантиметрах. Конечный результат – в квадратных метрах.

Если необходимо определит площадь прямоугольного или трапециевидного помещения, то есть у которого хотя бы одна пара сторон – параллельны друг другу, то для этого проще применить специальный калькулятор для четырехугольника. Он, кстати, учитывает возможное наличие выступов, колонн, ниш и других элементов, увеличивающих или уменьшающих общую площадь комнаты.

Существуют и более сложные случаи расчета площадей

Иногда приходится прибегать и к более сложным расчетам, когда некоторым стенам или элементам конструкции придана криволинейная форма. Как вычислить площадь комнаты при таких условиях – рассказывается в специальной публикации нашего портала.

Калькулятор треугольника

— Площадь в квадратных метрах

Что такое треугольник?

Треугольник — это особая замкнутая форма или многоугольник, имеющий три вершины, три стороны и три угла. Вершина — это точка пересечения двух линий или сторон. Поскольку у треугольника три стороны, у него также есть три вершины a, b и c. Сумма внутренних углов всегда составляет 180 °. Треугольник можно классифицировать по длине стороны и внутренним углам.

Например, треугольник с равной длиной сторон может быть идентифицирован как равносторонний треугольник или треугольник, ни одна из линий / сторон, имеющих одинаковую длину, не является равносторонним треугольником.

Треугольников, определяемых по длине сторон:

Треугольников, обозначенных углами:

Типы треугольника:

Треугольники можно разделить на 6 различных типов в зависимости от длины их сторон и углов.

1. Острый угловой треугольник:

   Треугольник, все три угла которого меньше 90 °.
   ∠ABC, ∠ACB и ∠BAC — все острые углы.

2. Прямоугольный треугольник:

   Треугольник с одним углом 90 °.
   ∠ABC = один прямой угол.

3. Тупоугольный треугольник:

   В тупом треугольнике любой из треугольников больше 90 °.
   ∠ABC

4. Равносторонний треугольник:

   Когда все стороны треугольника равны. Это называется равносторонним.
   Здесь AB = BC = CA.

5. Равнобедренный треугольник:

   Треугольник, у которого по крайней мере две стороны равной длины, называется равнобедренным треугольником.
   Здесь AB = AC.

6. Треугольник из шкалы:

   Треугольник, у которого все стороны разной длины.

Фактов о треугольнике:

У треугольника не может быть более одной стороны, больше или равной 90 °. Как упоминалось выше в определении треугольника, треугольник — это замкнутый путь.

Сумма всех внутренних треугольников всегда равна 180 °.

Сумма любых двух сторон всегда больше длины третьей стороны.

Теорема Пифагора:

Теорема Пифагора, это теорема о прямоугольном треугольнике. Согласно теореме Пифагора, квадрат длины на стороне гипотенузы (самой длинной стороне) равен сумме двух других сторон.Любой треугольник, удовлетворяющий этому условию, является прямоугольным.

Уравнение Пифагора:

a ² + b ² = c ²
EX: Если a = 5, c = 7, найти b:
5 ² + b ² = 7 ²
25 + b ² = 49
b ² = 24 => b = 4,8989

Закон синуса:

Согласно закону синусов, отношение длины стороны к синусу противоположного угла постоянно.Закон синусов помогает найти любую недостающую длину или угол треугольника. Например: если известны длины сторон а и углы А и В. Мы можем легко найти длину стороны b, подставив данную информацию в следующие формулы:

В случае, если известны все длины сторон, углы треугольников можно рассчитать следующим образом:

Как рассчитать площадь треугольника?

Существует множество методов вычисления площади треугольника. Выбор метода зависит от имеющейся информации.Самый распространенный метод определения площади треугольника:

В случае, если известны все длины сторон, углы треугольников можно рассчитать следующим образом:

В сценарии, где указаны две стороны и угол. Небольшое изменение формулы можно сделать, чтобы получить площадь треугольника. Формула будет:

Существует еще один метод вычисления площади треугольника с помощью формулы Герона, который требует, чтобы были известны все три стороны:

Медиана:

Медиана треугольника — это длина линии, проведенной от вершины треугольника до середины противоположной стороны.Треугольник имеет три медианы, которые пересекаются друг с другом в центре тяжести треугольника.

Центроид — это среднее арифметическое положение всех точек треугольника.

Ma = медиана стороны a
Mb = медиана стороны b
Mc = медиана стороны c
Медиана каждой стороны может быть рассчитана следующим образом:

Inradius:

Внутренний радиус — это радиус круга, нарисованного внутри треугольника, который касается всех трех сторон треугольника, то есть вписанного круга.Центр этого круга — это точка, в которой две биссектрисы пересекаются друг с другом. Он перпендикулярен любой из трех сторон треугольника.

Формула для вычисления inradius:
Inradius = Area / s
Где s = a + b + c / 2
Где a, b и c — длины сторон треугольника.

Круговой радиус:

В случае треугольника радиус описанной окружности — это радиус окружности, проходящей через все вершины треугольника. Центральная точка этого круга называется центром описанной окружности.Центр окружности — это точка, в которой все срединные перпендикуляры каждой стороны треугольника пересекаются.

Формула радиуса описанной окружности:
Окружной радиус = a / 2 * sin (A)
Где a — длина стороны, а A — угол, противоположный стороне a.
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.

Чтобы понять, как рассчитать квадратные метры, мы должны сначала начать с определения площади.Площадь — это размер двумерной поверхности. Площадь треугольника — это пространство, заключенное между его тремя сторонами. Чтобы узнать площадь треугольника, нам нужно знать длину трех его сторон. Стороны должны быть измерены в футах (футах) для расчета площади в квадратных футах и, при необходимости, преобразованы в дюймы (дюймы), ярды (ярды), сантиметры (см), миллиметры (мм) и метры (м).

Формула:
Площадь треугольника = (1/4) x √ [(a + b + c) x (b + ca) x (c + ab) x (a + bc)]
Длина стороны a (футы, дюймы, ярды, см, мм, м)
Длина стороны b (футы вниз, дюймы, ярды, см, мм, м)
Длина стороны c (футы, дюймы, ярды, см, мм, м)
Ответ = ((1/4) x √ [(a + b + c) x (b + ca) x (c + ab) x (a + bc)])
Сокращения площади блока: футов ² , дюймы ² , ярды ² , см ² , мм ² , м ²

Где это нужно в повседневной жизни?

Наш калькулятор треугольников поможет вам рассчитать площадь, необходимую для треугольной формы.Хотя мы рассмотрим наиболее распространенные варианты использования, например Вы можете знать две стороны и включенный угол, но хотели бы знать длину недостающей стороны. Мы также недавно добавили калькулятор прямоугольного треугольника, который также часто используется в сценарии, когда вы знаете две стороны треугольника, одна из которых составляет 90 ° Deg.

Какие измерения вам нужны?

Вам необходимо знать длину трех сторон треугольника в футах (футах), дюймах (дюймах), ярдах (ярдах), сантиметрах (см), миллиметрах (мм) или метрах (м).

Что вы можете рассчитать с помощью этого инструмента?

Вы можете вычислить площадь треугольника в квадратных футах, квадратных дюймах, квадратных ярдах, квадратных сантиметрах, квадратных миллиметрах и квадратных метрах. Да, наш инструмент такой классный.

Наш калькулятор дает возможность рассчитать точную стоимость материалов. Все, что вам нужно сделать, это ввести цену за единицу площади и вуаля, вы получите полную стоимость материалов в один клик!

Коэффициенты пересчета:

Для преобразования квадратных футов, квадратных дюймов, квадратных ярдов, квадратных сантиметров, квадратных миллиметров и квадратных метров вы можете использовать следующую таблицу преобразования.

ярдов.

Квадратные футы в квадратные ярды	умножьте 2 футов на 0,11111, чтобы получить 2
Квадратные футы в квадратные метры	умножьте 2 на 0,092903, чтобы получить 2
Квадратные ярды в квадратные футы	умножьте ярды 2 на 9, чтобы получить ft 2
Квадратные ярды в квадратные метры	умножить ярд 2 на 0.836127 получить м 2
Квадратные метры в квадратные футы	умножьте m 2 на 10,7639, чтобы получить ft 2
Квадратные метры в квадратные ярды	умножьте m 2 на 1,19599, чтобы получить yd 2
Квадратные метры в квадратные миллиметры	умножьте значение m 2 на 1000000, чтобы получить мм 2
Квадратные метры в квадратные сантиметры	умножьте значение m 2 на 10000, чтобы получить cm 2
Квадратные сантиметры в квадратные метры	умножьте значение cm 2 на 0.0001, чтобы получить мм 2
квадратные сантиметры в квадратные миллиметры	умножьте значение в см 2 на 100, чтобы получить мм 2
Квадратные миллиметры в квадратные сантиметры	умножьте значение 2 мм на 0,000001, чтобы получить см 2
Квадратные миллиметры в квадратные метры	умножьте значение 2 мм на 1000000, чтобы получить m 2

.

Методы калькуляции кругов и треугольников в плоской геометрии

Вписанные и описанные круги

Окружность может быть вписанной или описанной. Окружность, описывающая треугольник, проходит через вершины треугольника, в то время как окружность, вписанная в треугольник, касается трех сторон треугольника. Третья связь, соединяющая круги и треугольники, — это круг, вписанный в треугольник. Эта комбинация возникает, когда часть кривой касается одной стороны, и есть воображаемая касательная линия, идущая от двух сторон треугольника.Учитывая A, B и C как стороны треугольника и A как площадь, формула для радиуса окружности, описывающей треугольник, будет r = ABC / 4A, а для круга, вписанного в треугольник, будет r = A / S где S = (A + B + C) / 2.

Методы калькулятора для кругов и треугольников

Методы калькулятора для задач, связанных с кругами и треугольниками, больше связаны с алгеброй, тригонометрией и геометрией. Запоминание формул — вот что нужно. Вот содержание статьи.

• Круг, вписанный в треугольник
• Круг, описывающий треугольник
• Три касательные друг к другу окружности
• Площадь сектора
• Круг, вписанный в сектор
• Биссектриса треугольника
• Размеры сторон треугольника
• Хорда круга
• Точка вне треугольника

Задача 1: Круг, вписанный в треугольник

Стороны треугольника 8 см, 10 см и 14 см.Определите радиус вписанной окружности.

Расчетная техника

а. Используя формулу Герона, найдите площадь треугольника.

г. Найдите периметр треугольника.

г. Найдите радиус вписанной окружности.

Окончательный ответ: Радиус вписанной окружности составляет 2,45 сантиметра.

Задача 2: Окружность, описывающая равносторонний треугольник

Площадь круга, описывающего равносторонний треугольник, равна 250.45 квадратных метров. Какая площадь у треугольника?

Расчетная техника

а. Зная площадь круга, найдите радиус.

г. Найдите сторону равностороннего треугольника.

г. Найдите площадь равностороннего треугольника.

Окончательный ответ: Площадь равностороннего треугольника, вписанного в круг, составляет 103,59 квадратных метров.

Задача 3: Три окружности касаются друг друга

Расстояние между центрами трех окружностей, которые касаются друг друга снаружи, составляет 10, 12 и 14 единиц.Какова площадь самого большого круга?

Расчетная техника

а. Составьте три уравнения для трех неизвестных.

г. Составьте уравнения в виде системы.

г. Определите площадь наибольшего круга, используя наибольший радиус из шага 2.

Окончательный ответ: Площадь самого большого круга составляет 201,06 квадратных единиц.

Задача 4: Треугольник, вписанный в круг

Площадь треугольника, вписанного в круг, равна 39.19 квадратных сантиметров, а радиус описанной окружности равен 7,14 сантиметра. Если две стороны вписанного треугольника равны 8 и 10 сантиметрам соответственно, найдите третью сторону.

Расчетная техника

а. Решите для третьей стороны C.

Окончательный ответ: Длина третьей стороны 14,00 сантиметров.

Задача 5: Площадь сектора

Угол сектора круга составляет 300 градусов, а радиус — 15 сантиметров.Найдите площадь в квадратных сантиметрах.

Расчетная техника

а. Используйте формулу для определения площади сектора.

г. Перейти в радианный режим. Находясь в режиме радиан, введите Shift Answer и выберите знак градуса.

Окончательный ответ: Площадь сектора 598,05 квадратных сантиметра.

Задача 6: Круг, вписанный в сектор

Сектор описывает круг радиусом 8,00 сантиметров. Если центральный угол сектора составляет 80 градусов, какова площадь?

Расчетная техника

а.Решите для радиуса сектора.

г. Решите для области сектора.

г. Перейти в радианный режим. Находясь в режиме радиан, введите Shift Answer и выберите знак градуса.

Окончательный ответ: Площадь сектора 291,83 квадратных сантиметра.

Задача 7: Биссектриса треугольника

Дан треугольник ABC со сторонами AB = 30 сантиметров, BC = 36 сантиметров и AC = 48 сантиметров. Найдите расстояние от точки пересечения серединных перпендикуляров до стороны BC.

Расчетная техника

а. Точка пересечения серединных перпендикуляров — это радиус описанной окружности. Найдите площадь треугольника, используя формулу Герона.

г. Найдите радиус описанной окружности.

г. Используя теорему Пифагора, найдите пропущенное значение x.

Окончательный ответ: Расстояние от точки пересечения серединных перпендикуляров до стороны BC равно 15.92 сантиметра.

Задача 8: Измерение сторон треугольника

Периметр треугольника ABC составляет 400 сантиметров. Если угол A равен 30 градусам, а угол B равен 58 градусам, найдите размер стороны AC.

Расчетная техника

а. Предположим, что AC = 1, затем воспользуемся техникой синусоидального закона для определения сторон AB и BC. Переведите калькулятор в режим уравнения и введите следующие значения.

г. Найдите длину стороны переменного тока.

Окончательный ответ: Длина стороны АС 170.31 сантиметр.

Задача 9: Хорда круга

Круг площадью 1018 квадратных сантиметров разрезан на два сегмента хордой в 8 сантиметрах от центра. Найти отношение площади меньшей части к большей?

Расчетная техника

а. Найдите радиус круга.

г. Найдите площадь маленького сегмента.

г. Решите для большего сегмента.

e. Найдите соотношение между двумя сегментами.

Окончательный ответ: Соотношение между двумя сегментами составляет 0,293.

Задача 10: Точка вне треугольника

От точки за пределами равностороннего треугольника расстояния до вершин равны 10, 18 и 10 сантиметрам соответственно. Какова длина одной стороны треугольника?

Расчетная техника

а. Найдите длину одной стороны X, используя закон косинуса.

Окончательный ответ: Длина одной стороны треугольника равна 19.95 сантиметров.

.

Как рассчитать стороны и углы треугольников

Ниже приведены некоторые часто задаваемые вопросы о треугольниках.

Сколько градусов в треугольнике?

Сумма внутренних углов всех треугольников составляет 180 градусов.

Что такое гипотенуза треугольника?

Гипотенуза треугольника — его самая длинная сторона.

К чему складываются стороны треугольника?

Сумма сторон треугольника зависит от индивидуальной длины каждой стороны.В отличие от внутренних углов треугольника, которые всегда составляют 180 градусов

Как рассчитать площадь треугольника?

Чтобы вычислить площадь треугольника, просто используйте формулу:

Площадь = 1 / 2ач

«a» представляет длину основания треугольника. «h» представляет его высоту, которая определяется путем проведения перпендикулярной линии от основания до вершины треугольника.

Как найти третью сторону треугольника, которая неправильна?

Если вы знаете две стороны и угол между ними, используйте правило косинуса и подставьте значения для сторон b, c и угла A.

Затем найдите сторону a.

Затем используйте значение угла и правило синуса, чтобы найти угол B.

Наконец, используйте свои знания о том, что углы всех треугольников в сумме составляют 180 градусов, чтобы найти угол C.

Как найти недостающую сторону прямоугольного треугольника?

Используйте теорему Пифагора, чтобы найти недостающую сторону треугольника. Формула выглядит следующим образом:

c² = a² + b²

c = √ a² + b²

Как называется треугольник с двумя равными сторонами?

Треугольник с двумя равными сторонами и одной стороной, которая длиннее или короче других, называется равнобедренным треугольником.

Что такое формула косинуса?

Эта формула дает квадрат на стороне, противоположной углу, зная угол между двумя другими известными сторонами. Для треугольника со сторонами a, b и c и углами A, B и C три формулы:

a ² = b ² + c ² — 2bc cos A

или

b ² = a ² + c ² — 2ac cos B

или

c ² = a ² + b ² — 2ab cos C

Как рассчитать объем треугольника?

Поскольку треугольник является плоским и двумерным объектом, его объем невозможно определить.Треугольник плоский. Таким образом, у него нет объема.

Треугольные призмы, с другой стороны, представляют собой трехмерные объекты с определяемым объемом. Чтобы определить объем треугольной призмы, вы должны определить площадь основания призмы, а затем умножить ее на высоту. Формула выглядит следующим образом:

V = bh

В приведенной выше формуле «V» представляет объем, «b» представляет площадь основания треугольной призмы, а «h» представляет высоту треугольной призмы.

Как определить стороны треугольника, если я знаю все углы?

Вам нужно знать хотя бы одну сторону, иначе вы не сможете вычислить длины треугольника. Не существует уникального треугольника, у которого все углы одинаковы. Треугольники с одинаковыми углами похожи, но соотношение сторон у любых двух треугольников одинаковое.

Как вычислить стороны треугольника, если я знаю все стороны?

Используйте правило косинуса в обратном порядке.
Правило косинуса гласит:

c ² = a ² + b ² — 2ab cos C

Затем, переставив уравнение правила косинуса, вы можете вычислить угол

C = arccos ((a ² + b ² — c ² ) / 2ab)

и

B = arccos ((a ² + c ² — b ² ) / 2ac)

Третий угол A равен (180 — C — B)

.

Калькулятор прямоугольного треугольника | Определение

Тени и прямоугольники (радиус Земли)

Мы много говорили о треугольниках, в частности, о прямоугольных треугольниках и их применении в математике и геометрии. О чем мы еще не говорили, так это о полезности прямоугольных треугольников для расчетов в реальной жизни . Может показаться, что приложения за пределами геометрии ограничены, но давайте посмотрим на тени.

Да, тени. Темный оттенок, излучаемый объектом при его освещении.Если вы посмотрите на форму, образованную тенью, объектом и землей, вы заметите, что это, на самом деле, прямоугольный треугольник! По крайней мере, когда объект идеально вертикален, а земля горизонтальна. В большинстве случаев это так или, по крайней мере, достаточно близко. Это означает, что мы можем использовать калькулятор прямоугольного треугольника, чтобы находить различную информацию об объектах под солнцем. Посмотрим как.

Представьте, что у вас есть здание, высота которого нам нужна, но вы не можете измерить его напрямую, потому что оно слишком высоко, чтобы уронить рулетку сверху.Что вы можете сделать, это измерить длину тени на улице. Затем с помощью любого углового инструмента и листа бумаги вы можете найти угол между тенью и землей. Зная, что угол между зданием и землей составляет 90 °, вы можете ввести эти значения данных в сторону прямоугольного треугольника и в калькулятор угла и получить значение высоты здания.

Используя эту технику, вы можете измерить высоту многих объектов , если у вас есть яркий солнечный день или другие источники света для освещения объекта.Фактически, это было очень распространенным методом измерения в былые времена. Вероятно, самое интересное и умопомрачительное использование прямоугольных треугольников принадлежит Эратосфену, которому удалось использовать прямоугольные треугольники и тени для измерения радиуса Земли , и теперь мы собираемся объяснить, как он это сделал.

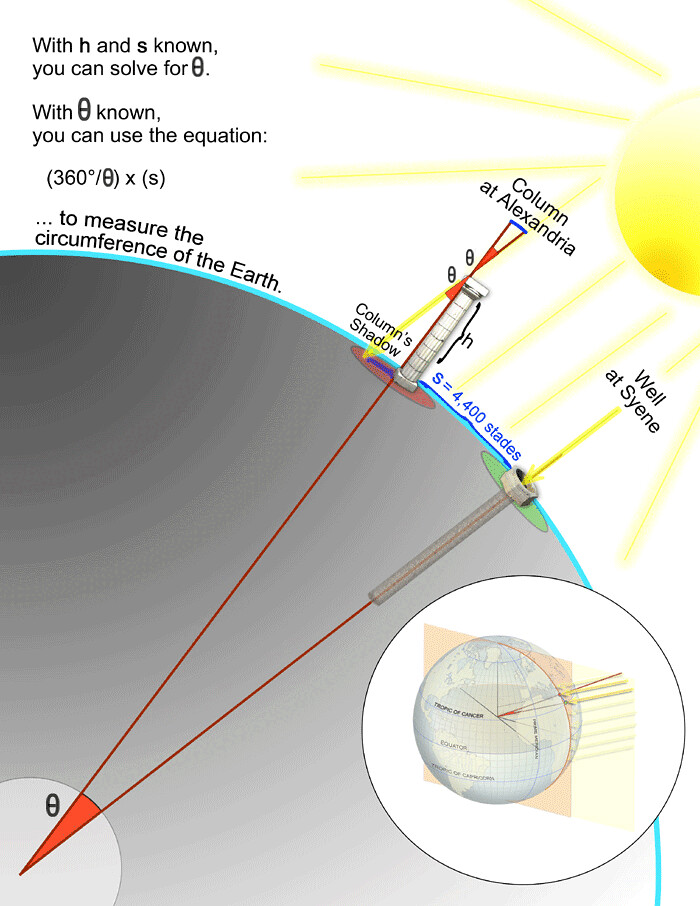
Эратосфен заметил, что в день летнего солнцестояния было место на Земле, где колодцы не имели тени в полдень, то есть солнце светило прямо на них.Заметив это, он установил колонну известной высоты на известном расстоянии от этого колодца и измерил размер тени в одно и то же время суток и в один и тот же день года в обоих местах. Затем, используя прямоугольные треугольники и тригонометрию, он смог измерить угол между двумя городами, а также радиус Земли , поскольку он знал расстояние между городами.

Это было поистине удивительное достижение, теперь вы можете сделать это намного проще, просто используя калькуляторы Omni, которые мы создали для вас .

Альваро Диес, Матеуш Муха и Петр Малек

.

Разное