Площадь неправильного прямоугольника: Калькулятор расчета площади земельного участка неправильной формы: четырехугольник

Инструкция для калькулятора расчета площади неправильного земельного участка

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Важно! Важ участок должен приблизительно вписываться в окружность. Иначе расчеты будут не совсем точными.

Указываем все данные в метрах

A B, D A, C D, B C— Размер каждой стороны делянки.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Методика определения размеров участка ручным методом

Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.

Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².

После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.

В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.

Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.

Общие данные

Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.

Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).

На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.

Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.

И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.

Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.

Считаем площадь неправильного 4-х угольника

Следующий калькулятор был создан по неоднократному запросу создать калькулятор, который бы смог считать площадь неправильного четырехугольника, в котором известны длины сторон.

Все мы понимаем, что данный четырехугольник может иметь любой вид (параллелограмма, квадрата, прямоугольника и так далее). Углы могут быть совершенно разные. По этому был создан уникальный калькулятор, который в реальном режиме прорисовывает четырехугольник и сразу считает его площадь, длины сторон нужно задать сразу вверху калькулятора, а потом нажать остановить на том четырехугольнике, площадь которого вы хотите посчитать.

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

Площадь четырехугольника

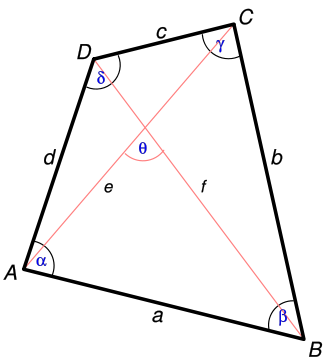
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

Таблица с формулами площади четырехугольника (в конце страницы)

— Вычисления   (показано)   (скрыто)

— примечания   (показано)   (скрыто)

Площадь четырехугольника по диагоналям и углу между ними

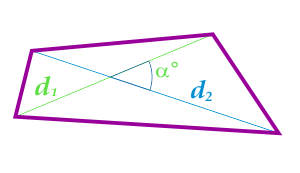
… подготовка …

d₁ — диагональ

d₂ — диагональ

α° — угол между диагоналями

Площадь четырехугольника через стороны и углы между этими сторонами

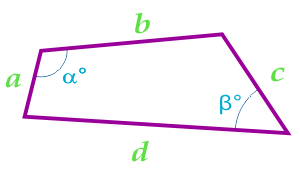
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

… подготовка …

a — сторона

b — сторона

c — сторона

d — сторона

α° — угол между сторонами

Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

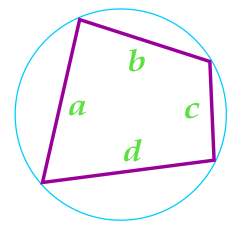
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

… подготовка …

b — сторона

c — сторона

d — сторона

Площадь четырехугольника в который можно вписать окружность

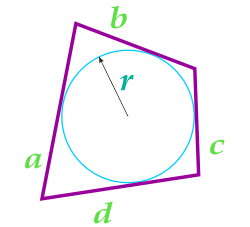
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

… подготовка …

a — сторона

b — сторона

c — сторона

d — сторона

r — радиус вписанной окружности

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

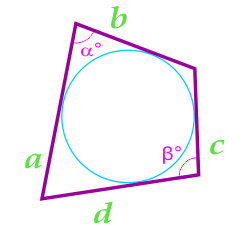
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

… подготовка …

a — сторона

b — сторона

c — сторона

d — сторона

α° — угол между сторонами

β° — угол между сторонами

Примечание:

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Таблица с формулами площади четырехугольника

Площадь частных случаев четырехугольников

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Онлайн калькулятор: Площадь четырехугольника

Есть несколько способов найти площадь неправильного четырехугольника.

Картинка: википедия

1. Вы знаете длины диагоналей и размер угла между ними. Тогда площадь четырехугольника можно найти по формуле
   

Калькулятор:

Площадь выпуклого четырехугольника

Знаков после запятой: 2

save Сохранить extension Виджет

2. Вы знаете длины четырех сторон и размеры двух противолежащих углов. Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.

,
где s — полупериметр.

Калькулятор:

Площадь четырехугольника по четырем сторонам и двум противолежащим углам

Знаков после запятой: 2

save Сохранить extension Виджет

3. Вы знаете длины четырех сторон и длины диагоналей. Тогда площадь четырехугольника тоже можно найти по формуле Бретшнайдера.

,
где s — полупериметр

Калькулятор:

Площадь четырехугольника по четырем сторонам и двум диагоналям

Знаков после запятой: 2

Расчет площади земельного участка неправильной формы

Итак, вы планируете продать свой участок. А может купить новый или присоединить соседний? В любом случае вам необходимо знать точный размер владений. Это поможет лучше сориентироваться в ценовом диапазоне и, что ещё важнее, правильно оформить документы на право собственности.

Итак, сколько квадратных метров в участке? Узнать это можно самостоятельно, не заказывая проект межевания у специалиста.

СодержаниеПоказать

Дорогие читатели! Для решения именно Вашей проблемы — звоните на горячую линию 8 (800) 350-34-85 или задайте вопрос на сайте. Это бесплатно.

Есть несколько способов произвести расчет площади земли, но самым точным является аналитический. Он выполняется с помощью формул площади по измеренным линиям границ. На этом способе и остановимся. Ведь линии границ у приусадебных или сельскохозяйственных угодий обычно чётко определены, а форма их зачастую представляет собой знакомую нам со школы фигуру — четырехугольник.

Вычисление площади по диагоналям и острому углу

Этот способ будет удобен в том случае, если участок слишком велик или непроходим для непосредственных измерений на местности, но имеется его вид сверху. Изображение на карте, на плане или даже фото с квадрокоптера.

Разумеется, для наиболее точных вычислений нужно как можно чётче выяснить масштаб. После этого нам понадобится измерить обе диагонали четырёхугольника (d1 и d2) и острый угол между ними (α).

Далее пользуемся формулой:

На калькуляторах манипуляции будут выглядеть так: сначала вводим величину острого угла, затем клавиша sin, перемножаем полученное число с данными о диагоналях и делим на два.

Активные граждане России часто интересуются, как получить землю на Дальнем Востоке.

Вам необходимо сделать межевание своего участка в СНТ? В нашей статье есть перечень необходимых документов, а также правильный порядок действий.

В российском законодательстве есть несколько форм права владения землей. Подробно о каждом из них написано здесь.

Вычисление площади по сторонам

Если же границы участка можно измерить вручную, тогда нам пригодится второй способ. Здесь нам нужны будут лишь длины всех четырех сторон (a,b,c,d). Сложив их вместе и поделив полученное число пополам, мы получим полупериметр нашего четырехугольника (p):

Далее используем эту величину, вычислив корень из перемножения её с её же разностями со всеми четырьмя сторонами:

Для верности конечно лучше сочетать оба эти способа. Результаты вычислений должны совпасть или быть очень близкими. Однако каждый из них достаточно надёжен, если пользоваться точно рассчитанными величинами.

Наибольшая трудность здесь очевидно в выяснении исходных данных. Впрочем, их можно перепроверить, запросив официальные земельные документы у властей или поискав на официальных административных ресурсах. Стоит учитывать, что там площадь участков будет отмечена в гектарах.

Не нашли ответа на свой вопрос? Звоните на телефон горячей линии 8 (800) 350-34-85. Это бесплатно.

Юрист. Практика в сфере недвижимости, тудового права, семейного права, защите прав потребителей

Формулы площадей всех основных фигур

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

 

Формула площади равнобедренной трапеции через стороны, (S):

 

Формула площади равнобедренной трапеции через стороны и угол, (S):

 

 

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α, β — углы трапеции

 

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

 

 

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α, β — углы между диагоналями

 

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

 

 

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α, β — углы при основании

 

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

 

 

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

 

Формула площади равнобедренной трапеции через основания и высоту, (S):

 

Площадь четырехугольника — формулы, примеры расчета

Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.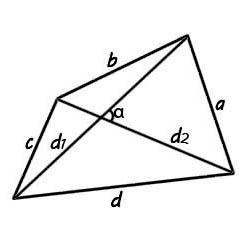

Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:

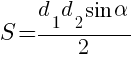
Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.

Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные: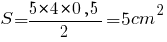

На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.

Площадь четырехугольника по сторонам

Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так: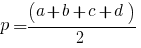
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр:

используем найденное значение для расчета площади:

Площадь четырехугольника, заданного координатами

Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.

Площадь неправильных форм

Чтобы найти область неправильной формы, первое, что нужно сделать, это разделить неправильную форму на правильные формы, которые вы можете распознать, например: треугольники, прямоугольники, круги, квадраты и пр.
Затем найдите область этих отдельных фигур и сложите их!

Пример №1:

Рисунок выше имеет две правильные формы. Он имеет квадрат и полукруг

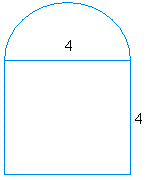
Найдите область для каждой из этих двух фигур и сложите результаты

Квадрат

Площадь _кв. = s ²

Площадь _кв. = 4 ²

Площадь _{квадрат} = 16

Круг

Площадь _круг = pi × r ²

Обратите внимание, что радиус круга равен 4/2 = 2

Площадь _круг = 3.14 × 2 ²

Площадь _{окружности} = 3,14 × 4

Область _{окружности} = 12,56

Поскольку у вас есть только полукруг, вы должны умножить результат на 1/2

1/2 × 12,56 = 6,28

Площадь этой формы = 16 + 6,28 = 22,28

Пример № 2: Рисунок выше имеет три правильные формы. Начиная сверху вниз, он имеет треугольник, прямоугольник, и трапеция

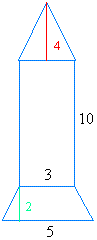
Найдите область для каждой из этих трех фигур и сложите результаты

Треугольник

Площадь _{треугольник} = (основание × высота) / 2

Площадь _{треугольник} = (3 × 4) / 2

Площадь _{треугольника} = 12/2

Площадь _{треугольника} = 6

Прямоугольник

Площадь _{прямоугольника} = длина × ширина

Площадь _{прямоугольника} = 3 × 10

Площадь _{прямоугольника} = 30

Трапеция

Площадь _{трапеция} = ((b ₁ + b ₂ ) × ч) / 2

Площадь _{трапеция} = ((3 + 5) × 2) / 2

Площадь _{трапеции} = (8) × 2/2

Площадь _{трапеции} = 16/2

Площадь _{трапеции} = 8

Площадь этой формы = 6 + 30 + 8 = 44

Пример № 3 :

Площадь неправильной формы может быть как как последний пример, поэтому внимательно изучите его!

Рисунок выше имеет 4 правильные формы.У него есть треугольник, два прямоугольника, и полукруга

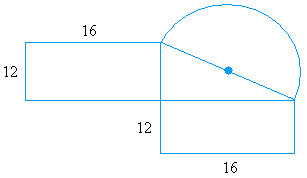
Найдите область для каждой из этих 4 фигур и сложите результаты

Прямоугольник

Площадь _{прямоугольника} = длина × ширина

Площадь _{прямоугольника} = (12 × 16)

Площадь _{прямоугольника} = 192

Поскольку у нас есть два одинаковых прямоугольника, площадь равна 192 + 192 = 384

Треугольник

Обратите внимание, что самая длинная сторона прямоугольника является основанием треугольника и короткой стороной прямоугольника. высота треугольника

Итак,

Площадь _{треугольника} = (основание × высота) / 2

Площадь _{треугольника} = (16 × 12) / 2

Площадь _{треугольника} = (192) / 2

Площадь _{треугольник} = 96

Круг

Чтобы получить площадь полукруга, нам нужно знать диаметр

Обратите внимание, что диаметр является гипотенузой прямоугольного треугольника, поэтому используйте пифагорейскую тео rem найти длину диаметра

c ² = a ² + b ²

c ² = 12 ² + 16 ²

c ² = 144 + 256

c ² = 400

c = √400

c = 20

Следовательно, диаметр равен 20.Поскольку диаметр равен 20, радиус равен 10

Площадь _{окружности} = pi × r ²

Площадь _{окружности} = 3,14 × 10 ²

Площадь _{окружности} = 3,14 × 100

Площадь _круг = 314

Так как у вас есть только половина круга, вы должны умножить результат на 1/2

1/2 × 314 = 157

Площадь этой формы = 384 + 96 + 157 = 637

Здесь мы идем! Я надеюсь, что эти хорошие примеры были очень полезны, помогая вам получить область неправильной формы.

Есть вопросы, как получить площадь неправильной формы? Свяжитесь со мной.

Новые уроки математики

Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.

,

Площадь неправильной формы | Shmoop

Площадь неправильной формы

В реальной жизни цифры часто бывают неправильной формы. — немного грязно. Подумайте еще раз о своей грязной спальне — это идеальный прямоугольник?

Хитрость: разбивает эти фигуры на фигуры, которые вы хорошо знаете (и чью область вы знаете, как найти) .

1. Найдите площадь этой комнаты:

Это можно сделать двумя различными способами:

2.Найдите площадь этой части баскетбольной площадки:

Эта фигура уже разделена на две фигуры: прямоугольник и полукруг.

Нам нужно найти площадь каждого и сложить их вместе.

3. Бассейн 20 футов x 12 футов должен быть окружен колодой шириной 6 футов. Сколько квадратных футов настила необходимо для этого?

Как всегда, мы хотим нарисовать картину того, как это выглядит.

Размеры большого внешнего прямоугольника:

Итак, площадь большего прямоугольника равна.

В эту сумму входит площадь бассейна, которую мы бы не хотели иметь настилом. Итак, вычтите площадь бассейна ().

Необходимое количество настилов:

.

Площадь неправильного многоугольника

Площадь неправильного многоугольника — Math Open Reference

В отличие от правильного многоугольника, если вы не знаете координаты вершин, нет простой формулы для площади неправильного многоугольника. Каждая сторона может иметь различную длину, и каждый внутренний угол может быть различным. Он также может быть выпуклым или вогнутым.

Если вы знаете координаты вершин многоугольника, есть два метода:

1. Ручной метод.См. Площадь многоугольника (Координатная геометрия).
2. компьютер алгоритм. См. Алгоритм, чтобы найти область любого многоугольника.

Так как это сделать?

Один из подходов состоит в том, чтобы разбить форму на части, которые вы можете решить — обычно треугольники, Так как существует много способов расчета площади треугольников. Как именно вы это делаете, зависит от того, что вам дано для начала. Поскольку это сильно варьируется, нет простого правила, как это сделать. Приведенные ниже примеры дают вам несколько основных подходов.

1. Разбейте на треугольники, затем добавьте

На рисунке выше, многоугольник можно разбить на треугольники, нарисовав все диагонали из одной из вершин. Если вы знаете достаточно сторон и углов, чтобы найти площадь каждой из них, то вы можете просто сложить их, чтобы найти общую сумму. Не бойтесь нигде рисовать дополнительные линии, если они помогут найти фигуры, которые вы можете решить.

Здесь неправильный шестиугольник делится на 4 треугольника путем добавления красных линий. (См. Площадь треугольника)

2.Найдите «пропущенные» треугольники, затем вычтите

На рисунке выше общая форма представляет собой правильный шестиугольник, но отсутствует треугольная фигура.

Мы знаем, как найти область правильного многоугольника, поэтому мы просто вычитаем площадь «пропущенного» треугольника, созданного рисованием красной линии. (См. Площадь правильного многоугольника и Площадь треугольника.)

3. Рассмотрим другие формы

На рисунке выше фигура представляет собой неправильный шестиугольник, но она имеет симметрию, которая позволяет разбить ее на два параллелограмма рисуя красную пунктирную линию.(при условии, конечно, что линии, которые выглядят параллельными, действительно есть!)

Мы знаем, как найти область параллелограмма, поэтому мы просто находим область каждого и складываем их вместе. (См. Площадь параллелограмма).

Как видите, существует бесконечное количество способов разбить фигуру на части, которыми легче управлять. Вы тогда добавляете или вычитаете области частей. То, как вы это делаете, зависит от личных предпочтений и того, что вам дают для начала.

4.Если вы знаете координаты вершин

Если вам известны координаты x, y вершин (углов) фигуры, существует метод непосредственного нахождения области. См. Площадь многоугольника (Координатная геометрия). Это работает для всех типов многоугольников (обычный, неправильный, выпуклый, вогнутый). Также есть компьютер алгоритм это делает то же самое. См. Алгоритм, чтобы найти область любого многоугольника.

Другие темы многоугольника

Общее

Типы полигонов

Площадь различных типов полигонов

Периметр различных типов многоугольников

Углы, связанные с полигонами

Именованные полигоны

(C) 2011 Copyright Math Открытая ссылка.
Все права защищены

,

Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора

Площадь — это размер поверхности!
Узнайте больше о площади или попробуйте калькулятор площади.

Пример: какова площадь этого прямоугольника?

формула:

Площадь = ш × ч
ш = ширина
ч = высота

Мы знаем с = 5 и с = 3 , поэтому:

Площадь = 5 × 3 = 15

Пример: какова площадь этого круга?

Радиус = r = 3

Площадь		= π × r 2
		= π × 3 2
		= π × (3 × 3)
		= 3.14159 … × 9
		= 28,27 (до 2 десятичных знаков)

Пример: какова площадь этого треугольника?

Высота = h = 12

База = b = 20

Площадь = ½ × b × h = ½ × 20 × 12 = 120

Более сложный пример:

Пример: Сэм подстригает траву по $ 0,10 за квадратный метр

Сколько зарабатывает Сэм, вырезая эту область:

Давайте разбить область на две части:

Часть A представляет собой квадрат:

Площадь А = ² = 20 м × 20 м = 400 м ²

Часть B — это треугольник.При взгляде сбоку он имеет основание 20 метров и высоту 14 метров.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м ²

Итак, общая площадь:

Площадь = Площадь А + Площадь B = 400 м ² + 140 м ² = 540 м ²

Сэм зарабатывает $ 0,10 за квадратный метр

Сэм зарабатывает = 0,10 × 540м ² = 54

,

Разное