Площадь четырехугольника — формулы, примеры расчета
Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.
Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:
Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см.
На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так:
используем найденное значение для расчета площади:
Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
В чем измеряется площадь прямоугольника. Площадь прямоугольника. Вычисляет площадь неправильного четырехугольника с известными длинами сторон
Площадь многоугольника
Понятие площади многоугольника будем связывать с такой геометрической фигурой, как квадрат. За единицу площади многоугольника будем принимать площадь квадрата со стороной, равной единице. Введем два основных свойства, для понятия площади многоугольника.
Свойство 1: Для равных многоугольников значения их площадей равны.
Свойство 2:
Любой многоугольник можно разбить на несколько многоугольников. При этом площадь исходного многоугольника равняется сумме площадей всех многоугольников, на которые разбит данный многоугольник.
Площадь квадрата
Теорема 1
Площадь квадрата определяется как квадрат длины его стороны.
где $a$ — длина стороны квадрата.
Доказательство.
Для доказательства нам необходимо рассмотреть три случая.
Теорема доказана.
Площадь прямоугольника
Теорема 2
Площадь прямоугольника определяется произведением длин его смежных сторон.
Математически это можно записать следующим образом
Доказательство.
Пусть нам дан прямоугольник $ABCD$, у которого $AB=b,\ AD=a$. Достроим его до квадрата $APRV$, длина стороны которого равняется $a+b$ (рис. 3).
Рисунок 3.
По второму свойству площадей имеем
\ \ \
По теореме 1
\ \
Теорема доказана.
Пример задач
Пример 1
Найти площадь прямоугольника со сторонами $5$ и $3$.
Что такое площадь и что такое прямоугольник
Площадь – это такая геометрическая величина, с помощью которой можно определить размер какой-либо поверхности геометрической фигуры.
На протяжении многих веков так повелось, что вычисление площади называли квадратурой. То есть, чтобы узнать площадь несложных геометрических фигур, достаточно было подсчитать количество единичных квадратов, которыми условно были покрыты фигуры. А фигуру, которая имела площадь, называли квадрируемой.
Поэтому, можно подвести итог, что площадь – это такая величина, которая показывает нам размер части плоскости, соединенной между собой отрезками.
Прямоугольник – это такой четырехугольник, у которого все углы прямые. То есть, четырехстороннюю фигуру, которая имеет четыре прямых угла и ее противоположные стороны равны, называют прямоугольником.
Как найти площадь прямоугольника
Самый простой способ нахождения площади прямоугольника – взять прозрачную бумагу, например кальку, или клеенку и расчертить ее на равные квадратики по 1 см, а потом приложить к изображению прямоугольника. Количество заполненных квадратиков и будет площадью в сантиметрах квадратных. Например, на рисунке видно, что прямоугольник попадает в 12 квадратов, значит, его площадь равна – 12 кв.
Но для нахождения площади больших объектов, например квартиры, необходим более универсальный способ, поэтому была доказана формула, чтобы найди площадь прямоугольника необходимо умножить его длину на ширину.
А теперь давайте попробуем записать правило нахождения площади прямоугольника в виде формулы. Обозначим площадь нашей фигуры буквой S, буква а – будет обозначать его длину, а буква b – ширину.
В итоге получаем вот такую формулу:
S = а * b.
Если наложить эту формулу на рисунок прямоугольника выше, то мы получим те же 12 кв.см, т.к. а = 4 см, b = 3 см, а S = 4 * 3 = 12 кв.см.
Если взять две идентичные фигуры, и наложить их одну на другую, то они совпадут, а будут называться равными. У таких равных фигур будут также равны их площади и периметры.
Зачем уметь находить площадь
Во-первых, если вы знаете, как найти площадь какой-либо фигуры, то с помощью ее формулы вы без проблем сможете решать любые задачи по геометрии и тригонометрии.
Во-вторых, научившись находить площадь прямоугольника, вы сначала сможете решать простые задачки, а со временем перейдете к решению более сложных, и научитесь находить площади фигур, которые вписаны в прямоугольник или около него.
В-третьих, зная такую простую формулу, как S = а * b, вы получаете возможность без проблем решать любые простые бытовые задачи (например, находить S квартиры или дома), а со временем и сможете применить их к решению сложных архитектурных проектов.
То есть, если совсем упростить формулу нахождения площади, то она будет выглядеть так:
П = Д х Ш,
Что обозначает П – это искомая площадь, Д – это ее длина, Ш – обозначает ее ширину, а х – является знаком умножения.
А известно ли вам, что площадь любого многоугольника можно условно разбить на определенное количество квадратных блоков, которые находятся внутри этого многоугольника? Какая разница между площадью и периметром
Давайте на примере попробуем понять разницу между периметром и площадью. Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.
Например, наша школа находится на участке, который огражден забором – суммарная длина этого забора будет периметром, а то пространство, которое находится внутри ограждения и является площадью.
Единицы измерения площади
Если периметр одномерный измеряется в линейных единицах, которыми являются дюймы, футы и метры, то S относится к двумерным исчислениям и имеет свою длину и ширину.
И измеряется S в квадратных единицах, таких, как:
Один квадратный миллиметр, где S квадрата имеет сторону, равную одному миллиметру;
Квадратный сантиметр, имеет S такого квадрата, у которого сторона равна одному сантиметру;
Квадратный дециметр равен S этого квадрата со стороной в один дециметр;
Квадратный метр имеет S квадрата, сторона которого равна одному метру;
И наконец, квадратный километр имеет S квадрата, сторона которого равна одному километру.
Для измерения площадей больших участков на поверхности Земли используют такие единицы, как:
Один ар или сотка – если S квадрата имеет сторону десять метров;

Задачи и упражнения
А теперь давайте рассмотрим несколько примеров.
На рисунке 62 нарисована фигура, которая имеет восемь квадратов и каждая сторона этих квадратов равна одному сантиметру. Поэтому S такого квадрата будет квадратный сантиметр.
Если записать, то это будет выглядеть так:
1 см2. А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.
Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:
Р см2.
Давайте рассмотрим прямоугольник, изображений на рисунке 63. Этот прямоугольник состоит из трех полос, а каждая такая полоска разбита на пять равных квадратов, имеющих сторону в 1 см.
Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.см.:
Рассмотрим следующий пример. На рисунке 64 изображен прямоугольник ABCD, ломаной линией KLMN он разбит на две части. Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2.
Теперь давайте найдем площадь всего прямоугольника:
Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2.
Теперь давайте найдем площадь всего прямоугольника:
Итак, берем три и умножаем на семь и получаем 21 кв.см:
3 7 = 21 кв.см. При этом 21 = 12 + 9.
И приходим к выводу, что площадь всей нашей фигуры равна сумме площадей ее отдельных частей.
Рассмотрим еще один пример. И так на рисунке 65 изображен прямоугольник, который с помощью отрезка АС разбит на два равных треугольника ABC и ADC
А так, как нам уже известно, что квадрат – это такой же прямоугольник, только имеющий равные стороны, то площадь каждого треугольника будет равняться половине площади всего прямоугольника.
Представим, что сторона квадрата равна а, то:
S = a a = a2.
Делаем вывод, что формула площади квадрата будет иметь такой вид:
А запись a2 называется квадратом числа а.
И так, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:
4 4, то есть 4 * 2 = 16 кв. см.
см.
Вопросы и задания
Найдите площадь фигуры, которая разбита на шестнадцать квадратов, сторона которых равна одному сантиметру.
Вспомните формулу прямоугольника и запишите ее.
Какие измерения нужно произвести, чтобы узнать площадь прямоугольника?
Дайте определение равным фигурам.
Могут ли иметь равные фигуры различные площади? А периметры?
Если вам известны площади отдельных частей фигуры, как узнать ее общую площадь?
Сформулируйте и запишите, чему равняется площадь квадрата.
Историческая справка
А известно ли вам, что древние люди в Вавилоне умели рассчитать площадь прямоугольника. Так же древние египтяне делали расчеты различных фигур, но так как точных формул они не знали, то вычисления имели небольшие погрешности.
В своей книге «Начала» знаменитый древнегреческий математик Евклид, описывает различные способы вычисления площадей разных геометрических фигур.
Мы уже познакомились с понятием площадь фигуры
, узнали одну из единиц измерения площади — квадратный сантиметр
. На уроке мы выведем правило, как вычислить площадь прямоугольника.
На уроке мы выведем правило, как вычислить площадь прямоугольника.
Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.
Например:
Мы можем определить, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см 2 каждая.
Тогда площадь прямоугольника будет равна 3*4=12 см 2 .
Этот же прямоугольник можно разбить на 3 полоски по 4 см 2 .
Тогда площадь прямоугольника будет равна 4*3=12 см 2 .
В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.
Найдем площадь каждого прямоугольника.
Рассмотрим прямоугольник АКМО.
В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:
Число 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.
Рассмотрим прямоугольник KDCO.
В прямоугольнике KDCO в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие
Число 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)
Обобщим: площадь прямоугольника равна произведению его длины и ширины.
Решите задачу.
Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина — 2см.
Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.
Запишем решение.
Ответ: площадь прямоугольника 18см 2
Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?
Можно рассуждать так. Поскольку площадь — это произведение длин сторон прямоугольника, поэтому надо вспомнить таблицу умножения. При умножении каких чисел получается ответ 18?
Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .
Решите задачу.
Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр.
Нам известны длина и ширина прямоугольника. Необходимо вспомнить, что для нахождения площади необходимо найти произведение его длины и ширины, а для нахождения периметра нужно сумму длины и ширины умножить на два.
Запишем решение.
Ответ: площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.
Решите задачу.
Длина прямоугольника 4см, а ширина — 3см. Чему равна площадь треугольника? (смотри рисунок)
Чтобы ответить на вопрос задачи, сначала надо найти площадь прямоугольника. Мы знаем, что для этого необходимо длину умножить на ширину.
Посмотрите на чертёж. Вы заметили, диагональ разделила прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника. Значит, надо 12 уменьшить в 2 раза.
Ответ: площадь треугольника 6 см 2 .
Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и учились применять это правило при решении задач на нахождение площади прямоугольника.
1. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. М., «Просвещение», 2012 год.
2. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.
3. М.И.Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011 год.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И.Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н.Рудницкая. Тесты. М., «Экзамен», 2012 (127с.)
2. Издательство «Просвещение» ()
1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Начертите возможные варианты прямоугольников, площадь которых 18 см 2 .
4. Составьте задание по теме урока для своих товарищей.
Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И.И.Зубаревой и А.Г.Мордковича
Тренажер к учебнику Г.В.Дорофеева и Л.Г.Петерсона
Определение и понятие площади фигуры
Чтобы лучше понять, что такое площадь фигуры, рассмотрим рисунок.Эта произвольная фигура разбита на 12 маленьких квадратика. Сторона каждого квадратика равна 1 см. А площадь каждого квадратика равна 1 квадратному сантиметру, что записывается так: 1 см 2 .
Тогда площадь фигуры равна 12 квадратным сантиметрам. В математике площадь обозначается латинской буквой S.
Значит, площадь нашей фигуры равна: S фигуры = 12 см 2 .
Площадь фигуры равна площади всех маленьких квадратиков, из которых она состоит!
Ребята, запомните!
Площадь измеряется квадратными единицами длины.
Единицы измерения площади:
1. Квадратный километр — км 2 (когда площади очень большие, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для того, чтобы измерять площадь участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики, когда рисуют фигуры в тетради).
4. Квадратный миллиметр — мм 2 .
Площадь треугольника
Рассмотрим два вида треугольников: прямоугольный и произвольный.Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны равны 7 см и 4 см.
Формула для расчета площади треугольника записывается так:
S прямоугольного треугольника АВС = ВС * СА: 2
S прямоугольного треугольника АВС = 7 см * 4 см: 2 = 14 см 2
Теперь рассмотрим произвольный треугольник.
Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см.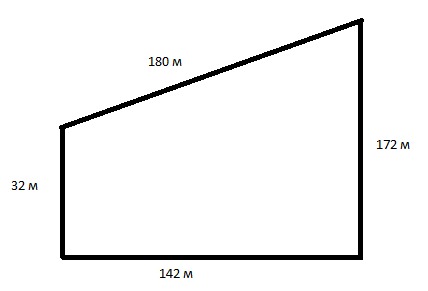 Как и в предыдущем примере, рассчитываем площадь по формуле:
Как и в предыдущем примере, рассчитываем площадь по формуле:
S произвольного треугольника АВС = ВС * h: 2.
Подставим в формулу наши данные и получим:
S произвольного треугольника АВС = 8 см * 6 см: 2 = 24 см 2 .
Площадь прямоугольника и квадрата
Возьмем прямоугольник АВСD со сторонами 5 см и 8 см.Формула расчета площади прямоугольника записывается так:
S прямоугольника АВСD = АВ * ВС.
S прямоугольника АВСD = 8 см * 5 см = 40 см 2 .
Теперь рассчитаем площадь квадрата. В отличии от прямоугольника и треугольника, для нахождения площади квадрата необходимо знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см. S квадрата АВСD = АВ * ВС = АВ 2 .
Подставим в формулу наши данные и получим:
S квадрата АВСD = 9 см * 9 см = 81 см 2 .
Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. Особая роль отводится площади прямоугольника, так как эта фигура одна из наиболее простых в изучении. 2$.
2$.
Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.
Средняя оценка: 4.4 . Всего получено оценок: 267.
Как найти площадь треугольника — Лайфхакер
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.

- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Сейчас читают 🔥
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.

- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.

- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
Формулы площади треугольника
Формулы площади треугольника
Подождите пару секунд пока подгрузятся формулы
Внимание! Десятичную дробь надо писать с точкой(.), а не с запятой!
Через основание и высоту
$$S= \frac{1}{2} ah $$ \(S\) — площадь треугольника\(a\) — основание
\(h\) — высота
\(a =\) \(h =\)
Через две стороны и угол
$$S= \frac{1}{2} ab sin \alpha $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\( \alpha \) — угол между сторонами \(a\) и \(b\)
\(a =\) \(b =\) \( \alpha =\)
Формула Герона
$$S= \sqrt{p(p-a)(p-b)(p-c)} $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(c =\)
Через радиус вписанной окружности
$$S= rp $$ \(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(r =\) \(p =\)
Через радиус описанной окружности
\(S= \frac{abc}{4R} \)\(S\) — площадь треугольника
\(R\) — радиус описанной окружности
\(a\) — сторона
\(b\) — сторона
\(c\) — сторона
\(a =\) \(b =\)
\(c =\) \(R =\)
Площадь прямоугольного треугольника
$$S= \frac{1}{2} ab $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(a =\) \(b =\)
Площадь прямоугольного треугольника
$$S= de $$ \(S\) — площадь треугольника\(d =\) \(e =\)
Формула Герона для прямоугольного треугольника
$$ S= (p-a)(p-b) $$ \(S\) — площадь треугольника\(a\) — сторона
\(b\) — сторона
\(p\) — полупериметр, \(p= \frac{a+b+c}{2}\)
\(a =\) \(b =\) \(p =\)
Площадь равнобедренного треугольника
$$S= \frac{1}{2} a^2 sin \alpha$$ \(S\) — площадь треугольника\(a\) — сторона
\(\alpha\) — угол между боковыми сторонами
\(a =\) \( \alpha =\)
Площадь равнобедренного треугольника
\(a\) — сторона
\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(a =\) \(b =\) \( \alpha =\)
Площадь равнобедренного треугольника
$$S= \frac{b^2}{4tg \frac{ \alpha }{2}} $$ \(S\) — площадь треугольника\(b\) — сторона
\(\alpha\) — угол между боковыми сторонами и основанием
\(b =\) \(\alpha =\)
Формула Герона для равнобедренного треугольника
a = b =Площадь равностороннего треугольника
$$S= \frac{ \sqrt{3}a^2}{4} $$ \(S\) — площадь треугольника\(a\) — сторона
\(a =\)
Площадь равностороннего треугольника
$$S= \frac{3 \sqrt{3}R^2}{4}$$ \(S\) — площадь треугольника\(R\) — радиус описанной окружности
\(R =\)
Площадь равностороннего треугольника
$$S= 3 \sqrt{3}r^2 $$ \(S\) — площадь треугольника\(r\) — радиус вписанной окружности
\(r =\)
Площадь равностороннего треугольника
$$S= \frac{h^2}{\sqrt{3}}$$ \(S\) — площадь треугольника\(h\) — высота
\(h =\)
Урок 14.
 измерение площади фигуры с помощью палетки — Математика — 4 класс
измерение площади фигуры с помощью палетки — Математика — 4 класс
Математика, 4 класс
Урок №14. Измерение площади фигуры с помощью палетки
Перечень вопросов, рассматриваемых в теме:
Площадь геометрической фигуры.
Вычисление площади фигур произвольной формы, используя палетку.
Глоссарий по теме:
Площадь — свойство фигур занимать место на плоскости.
Длина — свойство предмета “быть протяжённым в пространстве”
Палетка — прозрачная пластинка, разделенная на единицы площади.
Основная и дополнительная литература по теме урока:
- Математика: 4 класс: учебник в 2 ч. Ч.1/ М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова – М. Просвещение, 2016. – с. 36-38
- Всероссийские проверочные работе. Математика. Рабочая тетрадь 4 класс в 2 ч. Ч 1/ под.ред. Н.А. Сопруновой – М.; Просвещение, 2016. – с. 50 -68
Теоретический материал для самостоятельного изучения
Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.
Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см2
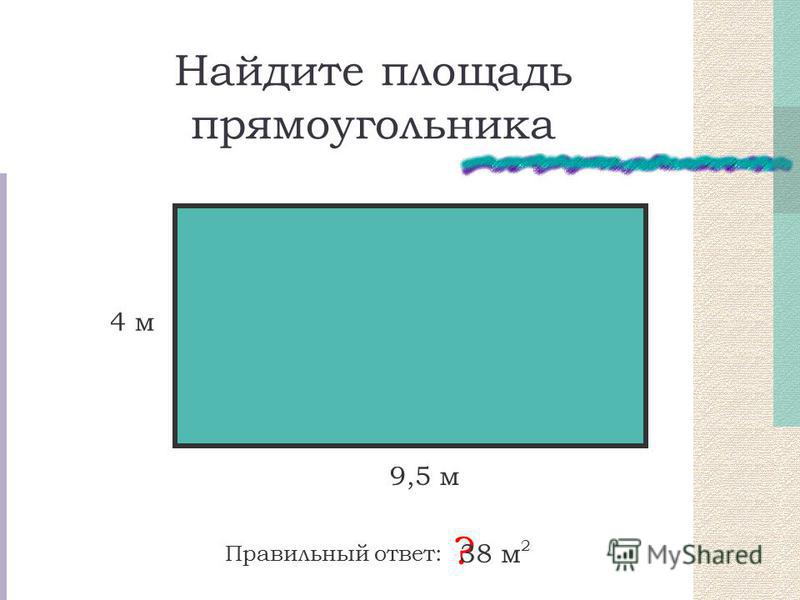
А теперь попробуйте вычислить площадь данной фигуры:
-?
Сегодня мы узнаем, что для нахождения площади фигур можно использовать палетку. Палетка – это прозрачная плёнка, которая может быть разбита на квадратные дециметры, квадратные сантиметры, квадратные миллиметры. Простейшая палетка — лист кальки, разделенный на квадратные сантиметры. Палетку используют для измерения площади фигур, ограниченных кривой линией.
Чтобы найти площадь данной фигуры, нужно:
1) На данную фигуру наложить палетку. Не сдвигать!
2)Сосчитать, сколько целых клеток- квадратных единиц — содержится в фигуре.
Целых 34 клетки.
3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.
Неполных 8 клеток.
4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.
8 : 2 = 4
5) Сложить числа, полученные в пунктах 2 и 4.
6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.
S = 34 + (8 : 2) = 38 см2
Ответ: S = 38 см2
Задания тренировочного модуля:
1. Определите, какая фигура имеет большую площадь, а какая — меньшую, и решите ребус соответствия.
Правильный ответ: Прямоугольник – большую, круг – меньшую.
Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.
Правильный ответ:
Площадь 7 см2
Периметр 12 см
|
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон. Сумма углов выпуклого четырёхугольника равна 360°: ∠A+∠B+∠C+∠D=360°. Не существует четырёхугольников, у которых все углы острые или все углы тупые. Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов: ∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D, ∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D. Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон: a < b+c+d, b < a+c+d, c < a+b+d, d < a+b+c. Площадь произвольного выпуклого четырёхугольника равна: |
||
|
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины. Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет. Площадь произвольного выпуклого четырёхугольника: |
||
|
Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона. Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны; SABCD = 2SMNPQ . |
||
|
Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника. В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам: MG=GP, NG=GQ, RG=GS . Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей: MP2+ NQ2+ RS 2 = ¼(AB2+BC2+CD2+AD2+AC2+BD2). Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь: SABCD = MP·NQ·sinβ. |
||
|
|
||
|
Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости. |
||
|
Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной. Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны: a+c = b+d. Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно: a+c ≥ 4r, b+d ≥ 4r. Площадь описанного четырёхугольника: S = pr, где r – радиус вписанной окружности, p – полупериметр четырёхугольника. Площадь описанного четырёхугольника: |
||
|
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника. Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника: AK=AN, BK=BL, CL=CM, DM=DN. Если O – центр окружности, вписанной в четырёхугольник ABCD, то ∠AOB+∠COD=∠BOC+∠AOD=180°. Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения: |
||
|
Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника. Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°: ∠A+∠C=∠B+∠D=180°. Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника. |
||
|
Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Радиус окружности, описанной около четырёхугольника: Площадь вписанного четырёхугольника: |
||
|
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами. Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов. У вписанного четырёхугольника любые два связанных угла равны. |
||
|
Если четырёхугольник одновременно является описанным и вписанным, то его площадь: Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение: |
||
|
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны: AB||CD, BC||AD. У параллелограмма противолежащие стороны равны и противолежащие углы равны: AB=CD, BC=AD; ∠A=∠C, ∠B=∠D. Сумма любых двух соседних углов параллелограмма равна 180°: ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°. |
||
|
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам: AO=OC; BO=OD. Каждая диагональ делит параллелограмм на два равных треугольника: ∠ABC=∠CDA; ∠ABD=∠CDB. Две диагонали параллелограмма делят его на четыре равновеликих треугольника: SΔABO=SΔBCO=SΔCDO=SΔADO. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: e2+f2 = a2+b2+a2+b2 = 2(a2+b2). |
||
|
Признаки параллелограмма:
|
||
|
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне: ha = b·sin γ; hb = a·sin γ. Площадь параллелограмма можно определить:
S = aha = bhb;
S = ab·sin γ. |
||
|
Ромбом называется параллелограмм, у которого все стороны равны: AB=BC=CD=AD. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов: AC⊥BD; ∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA. |
||
|
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности, вписанной в ромб, можно вычислить:
Площадь ромба можно определить:
|
||
|
Прямоугольником называется параллелограмм, у которого все углы прямые: ∠A=∠B=∠C=∠D=90°. |
||
|
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка: AC=BD; AO=BO=CO=DO. Площадь прямоугольника можно определить:
S = ab;
S = ½d²·sin γ. |
||
|
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали: BD = 2R. |
||
|
Квадрат – это прямоугольник, у которого все стороны равны: ∠A=∠B=∠C=∠D=90°, AB=BC=CD=AD. |
||
|
Диагонали квадрата равны и перпендикулярны. Сторона и диагональ квадрата связаны соотношениями: Площадь квадрата: |
||
|
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей. Радиус описанной окружности: Радиус вписанной окружности: |
||
|
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны: AD||BC. Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами. Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции. |
||
|
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции: AK=KB; CL=LD. Средняя линия трапеции параллельна её основаниям и равна их полусумме: KL||AD; KL||BC; KL = ½(AD+BC). |
||
|
При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ: ΔAED∼ΔBEC, k=AD/BC. Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ: ΔAОD∼ΔCОВ, k=AD/BC. Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: SΔABO = SΔCDO. |
||
|
Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон: O∈KL; E∈KL. Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности: RS||AD; RS||BC; RS = ½(AD–BC). |
||
|
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон: AD+BC=AB+CD. Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции. В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств: Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом: ∠AOB=∠COD=90°. Радиус вписанной в трапецию окружности можно определить:
|
||
|
Равнобокой называется трапеция, у которой боковые стороны равны: AB=CD. У равнобокой трапеции:
AC=BD;
∠A=∠D, ∠B=∠C;
∠A+∠C=∠B+∠D=180°. Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая. Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c². |
||
|
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям. |
||
|
Площадь трапеции можно определить:
|
||
|
Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон. Дельтоид может быть выпуклым или невыпуклым. Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом. В любом дельтоиде углы между соседними неравными сторонами равны. Площадь любого дельтоида можно определить:
S = ab·sin α . |
||
|
В любой выпуклый дельтоид можно вписать окружность. Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида. Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины. |
||
|
Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°. Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
|
||
|
Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом. Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
|
||
|
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности: a²+c² = b²+d² = 4R². |
||
|
Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны: ac = bd. Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О, то верны соотношения: |
||
формулы площади, доказательства.
 Трапеция на занятиях с репетитоом по математике — Колпаков Александр Николаевич
Трапеция на занятиях с репетитоом по математике — Колпаков Александр Николаевич
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы :). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве, подготовка к ЕГЭ в Строгино.
Площадь неправильных форм — формула, примеры, определение
Площадь неправильных форм означает площадь, занимаемую фигурой, которая измеряется в квадратных единицах. Неправильная форма может быть любого размера и длины. Вокруг нас можно увидеть неправильные формы, например, воздушного змея, ромбовидную форму, лист и т. д. Любая форма, стороны и углы которой не имеют одинаковой длины, называется неправильной формой.
Какова площадь неправильных фигур?
Площадь неправильной формы — это площадь области, покрытой этой формой.Неправильные формы – это фигуры, у которых не равны ни стороны, ни углы. Чтобы найти площадь неправильной формы, ее можно разложить или разделить на несколько знакомых фигур, а затем добавить их площадь, чтобы получить общую площадь. Мы можем видеть различные примеры неправильных форм в нашей повседневной жизни:
- Осмотрите лестницу здания.
 Поверхность лестницы имеет неправильную форму, состоящую из многоугольников, таких как прямоугольники и квадраты.
Поверхность лестницы имеет неправильную форму, состоящую из многоугольников, таких как прямоугольники и квадраты. - Детская площадка в школе с беговой дорожкой имеет неправильную форму, а также представляет собой комбинацию правильных форм.
- Лист растения неправильной формы.
Единица площади неправильной формы выражается в м 2 , см 2 , в 2 или в футах 2 .
Как найти площадь неправильной формы?
Чтобы найти площадь неправильной формы, мы должны знать, как разложить неправильную форму на знакомые формы.
Разложить неправильную форму
Следующая фигура представляет собой неправильную фигуру, площадь которой не может быть рассчитана по определенной формуле.Если мы разложим его, то увидим, что его можно разделить на многоугольники P, Q, R, S, T и U. Другими словами, эти многоугольники соединяются вместе, образуя неправильную форму. Итак, после разложения мы находим площадь этих многоугольников и складываем значения, чтобы получить площадь заданной неправильной формы.
Итак, после разложения мы находим площадь этих многоугольников и складываем значения, чтобы получить площадь заданной неправильной формы.
Возьмем другой пример. Данную фигуру можно разделить на несколько многоугольников A, B, C, D, E, F и G. Поскольку мы распознаем эти формы, мы можем легко найти их площадь и сложить их, чтобы получить площадь данной неправильной формы. .
Формула для нахождения площади неправильных фигур
Прямой формулы для вычисления площади неправильной формы не существует. В таких случаях мы используем разные методы для нахождения площади.
Метод 1: Как мы обсуждали ранее, чтобы найти площадь неправильной формы, мы можем разделить неправильную форму на знакомые многоугольники, а затем найти площадь каждого отдельного многоугольника.
Следовательно, площадь заданной неправильной формы = площади всех многоугольников, образующих неправильную форму.
⇒ Площадь заданной неправильной формы = площадь А + площадь В + площадь С + площадь D + площадь Е + площадь F + площадь G
Метод 2: В некоторых случаях неправильная форма делится на небольшие квадраты или сетки. Общее количество единичных квадратов, попадающих в фигуру, определяет общую площадь. Следует отметить, что при расчете площади для более точной оценки квадрат считается за «1», если заштрихованная область покрывает более половины каждого квадрата.Итак, в этом случае мы получаем приблизительную площадь неправильной формы. Мы можем использовать этот метод для фигур, которые имеют кривые, как показано на следующем рисунке.
Общее количество единичных квадратов, попадающих в фигуру, определяет общую площадь. Следует отметить, что при расчете площади для более точной оценки квадрат считается за «1», если заштрихованная область покрывает более половины каждого квадрата.Итак, в этом случае мы получаем приблизительную площадь неправильной формы. Мы можем использовать этот метод для фигур, которые имеют кривые, как показано на следующем рисунке.
Следовательно, площадь данной неправильной формы = Сумма всех единичных квадратов, попадающих под неправильную форму.
Часто задаваемые вопросы об области неправильных форм
Какова площадь неправильных фигур?
Площадь неправильных форм определяется как количество пространства, которое покрыто неправильными формами.Неправильные формы – это фигуры, у которых не равны ни стороны, ни углы. Единица площади неправильной формы выражается в квадратных единицах, например, м 2 , см 2 , в 2 или в футах 2 .
Чем площадь неправильной формы отличается от площади правильной формы?
Правильная форма имеет равные стороны и углы, тогда как неправильная форма может быть любого размера и длины. Таким образом, площадь правильной формы можно определить, непосредственно применяя к ней подходящие формулы, тогда как площадь неправильной формы можно найти, разложив неправильную форму на несколько правильных фигур.
Есть ли формула для нахождения площади неправильной формы?
Не существует специальной формулы для нахождения площади неправильной формы, поскольку у неправильной формы все стороны разной длины. Иногда неправильная форма состоит из комбинации многоугольников, поэтому формула определяется путем разложения неправильной формы на правильные формы.
Как найти площадь неправильной формы?
Мы можем найти площадь неправильной формы, используя следующие шаги:
- Шаг 1: Разложите неправильную форму на знакомые многоугольники.

- Шаг 2: Найдите сумму площадей всех известных многоугольников, чтобы найти площадь неправильной формы.
Как найти площадь неправильной формы методом единичного квадрата?
Мы можем найти площадь неправильной формы, используя метод единичного квадрата со следующими шагами:
- Шаг 1: Разделите заданную неправильную форму на маленькие квадраты, равные единице квадратной площади.
- Шаг 2: Общее количество единичных квадратов, попадающих в фигуру, определяет общую площадь.
- Шаг 3: При расчете площади для более точной оценки посчитайте квадрат за «1», если заштрихованная область покрывает более половины каждого квадрата.
Является ли метод единичного квадрата точным способом нахождения площади неправильных фигур?
Нет, при измерении площади неправильной формы методом единичного квадрата вместо точного значения мы получаем приблизительное значение площади.
Площадь параллелограмма ИЛИ Площадь неправильной формы – Площадь в квадратных футах
В чем разница между правильной и неправильной формой?
Правильная форма: Все стороны и углы правильных фигур равны.
Неправильная форма: Стороны и углы неправильной формы могут быть любой длины и размера.
Как вычислить площадь неправильной формы?
Теперь, когда мы знаем разницу между правильными и неправильными формами. Давайте упростим наш процесс расчета, разделив неправильную форму на правильные формы. Посмотрите пример ниже, здесь мы разделили фигуры на треугольники, которые имеют правильную форму.
Затем вы можете легко вычислить площадь каждого треугольника с помощью формулы Герона.
После вычисления площади каждого треугольника просто сложите их все, чтобы найти площадь неправильной формы.
Как использовать калькулятор неправильной площади?
Шаг 1: Измерьте все стороны области в одной единице (футы, метры, дюймы или любые другие).
Шаг 2: Введите длину горизонтальных сторон в поля «Длина 1» и «Длина 2». И ширину вертикальных сторон в поля «Ширина 1» и «Ширина 2». (См. изображение выше).
изображение выше).
Шаг 3: Нажмите кнопку расчета.Вывод, который дает наш калькулятор, не зависит от единицы измерения. Например, если вы ввели значения в футах. Вывод всегда будет в футах.
Наша формула: Площадь = b × h
Сокращения единиц площади:
футов 2 =
квадратных футовВ 2 = квадратные дюймы
ярда 2 =
квадратных ярдасм 2 = квадратные сантиметры
мм 2 = квадратные миллиметры
M 2 = Квадратные метры
Шаг 1: Определите все стороны неправильной формы. Убедитесь, что все стороны имеют одинаковый размер.
Шаг 2: Нарисуйте площадь на листе бумаги, используя полученные измерения. Помните, что ваш рисунок должен быть в масштабе.
Шаг 3: Разделите рисунок на разные фигуры. Простые — это квадрат и прямоугольник, круги и треугольник могут быть немного сложными.
Шаг 4: Рассчитайте площадь каждой фигуры с помощью нашего калькулятора площади в квадратных футах. Для прямоугольников и квадратов умножьте ширину на высоту. Для треугольников умножьте основание на высоту, а затем разделите на 2.Для кругов умножьте квадрат радиуса на 3,14 (пи). Радиус круга — это расстояние от его центра до любой другой точки на краю круга.
Шаг 5: Сложите площади всех отдельных фигур, чтобы найти общую площадь в квадратных футах.
Наша формула: Площадь = b × h
Коэффициенты пересчета:
Для преобразования между квадратными футами, квадратными дюймами, квадратными ярдами, квадратными сантиметрами, квадратными миллиметрами и квадратными метрами вы можете использовать следующую таблицу преобразования.
| Квадратные футы в Ярды | умножьте ft 2 на 0,11111, чтобы получить yd 2 |
| Квадратные футы в Метры | умножьте ft 2 на 0,092903, чтобы получить m 2 |
| Квадратные ярды в квадратные футы | умножьте ярды 2 на 9, чтобы получить футы 2 |
| Квадратные ярды в Квадратные метры | умножьте yd 2 на 0,836127, чтобы получить m 2 |
| Квадратные метры в Квадратные футы | умножьте m 2 на 10. 7639, чтобы получить футов 2 7639, чтобы получить футов 2 |
| Квадратные метры в Квадратные ярды | умножьте м 2 на 1,19599, чтобы получить ярды 2 |
| Квадратные метры в квадратные миллиметры | умножьте значение m 2 на 1000000, чтобы получить мм 2 |
| Квадратные метры в Квадратные сантиметры | умножьте значение m 2 на 10 000, чтобы получить см 2 |
| Квадратные сантиметры в Квадратные метры | умножьте значение cm 2 на 0.0001 получить мм 2 |
| Квадратные сантиметры в Квадратные миллиметры | умножьте значение см 2 на 100, чтобы получить мм 2 |
| Квадратные миллиметры в квадратные сантиметры | умножьте значение мм 2 на 0,000001, чтобы получить см 2 |
| Квадратные миллиметры в Квадратные метры | умножьте значение мм 2 на 1000000, чтобы получить m 2 |
Площадь неправильных форм — расчеты, примеры и часто задаваемые вопросы
Неправильные формы — это многоугольники с пятью или более сторонами различной длины. Эти формы или фигуры могут быть далее разложены на известные формы, такие как треугольники, квадраты и четырехугольники, для оценки площади.
Эти формы или фигуры могут быть далее разложены на известные формы, такие как треугольники, квадраты и четырехугольники, для оценки площади.
Некоторые примеры неправильной формы:
Предметы повседневной жизни неправильной формы
Как рассчитать площадь неправильной формы?
Определение площади неправильных форм
Существуют следующие методы оценки площади неправильной формы:
-
Оценка площади с использованием единичных квадратов.
-
Разделение неправильной формы на две или более правильных фигур.
-
Разделение неправильной формы с кривыми на две или более правильных форм.
Как найти площадь неровной фигуры?
Оценка площади с помощью единичных квадратов
Мы можем использовать этот метод для форм с кривыми, кроме идеального круга или полукруга и неправильных четырехугольников. В этом методе мы сначала делим фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в фигуру, используется для определения общей площади.
В этом методе мы сначала делим фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в фигуру, используется для определения общей площади.
Например: Рассчитайте площадь, посчитав единичные квадраты на приведенном ниже рисунке.
Ответ: Если мы обозначим каждую единицу квадрата в сантиметрах, площадь будет 6 см 2 .
Вычисление площади неправильной формы с изогнутыми краями
Разделение неправильной формы на две или более правильных фигур
Используйте этот метод для вычисления площади неправильных фигур, представляющих собой комбинацию треугольников и многоугольников.Используя заранее определенные формулы, вычислите площадь таких фигур и сложите их вместе, чтобы получить общую площадь.
Например, в приведенной ниже неправильной форме мы разделим несколько ребер на треугольник и три многоугольника.
Общая площадь фигуры может быть рассчитана путем сложения отдельных площадей:
Общая площадь = Площадь (ABIM) + Площадь (BCGH) + Площадь (CDEF) + Площадь (JKL)
⇒ Общая площадь = (AB × BI ) + (BC × CG) + (CD × DE) + (12 × LJ × KO)
⇒ Общая площадь = ( 10 × 5) + (3 × 3) + (2 × 2) + (1⁄2 × 4 × 4)
⇒ Общая площадь = 50 + 9 + 4 + 8
⇒ Общая площадь = 71 см 2
Вычисление площади неправильной формы
кривые в две или более правильных форм.
В этом методе можно разделить неправильную форму на несколько квадратов, треугольников или других четырехугольников. В зависимости от формы или кривых, часть фигуры может быть также кругом, полукругом или квадрантом.
Найдите площади заданной неправильной формы с 8 сторонами, включая одну кривую.
Сол: Определим неизвестные величины по заданным размерам сторон. Сначала нам нужно разделить фигуру на два прямоугольника и полукруг.
Сначала нам нужно разделить фигуру на два прямоугольника и полукруг.
Площадь фигуры ABCDEF равна:
Общая площадь (ABCDEF) = Площадь (ABCG) + Площадь (GDEF) + Площадь (aob)
Общая площадь = (AB × AG) + (GD × DE) + ( 1⁄2 × π × ob 2 )
Общая площадь = (3 × 4) + (10 × 4) + (1/2 × 3.14 × 12)
Общая площадь = 12 + 40 + 1,57
Следовательно, общая площадь = 53,57 см 2
Как найти площадь неправильной формы с помощью миллиметровой бумаги?
Какова площадь неровной поверхности?
Найдите площадь данного листа.
Решение: Чтобы найти площадь неровной поверхности в приведенном выше примере листа, мы должны положить лист на миллиметровую бумагу и провести его границу.
Форма листа неправильная. Итак, мы предположим, что более половины квадрата, покрытого листом, будет считаться за 1, а меньше этого будет считаться за 0.
Итак, мы предположим, что более половины квадрата, покрытого листом, будет считаться за 1, а меньше этого будет считаться за 0.
Теперь подсчитайте количество полностью закрытых фигур. Полностью покрыты 64 квадрата.
Кроме того, посчитайте частично более чем наполовину закрытые клетки, и каждая будет считать qs 1 клетку. Есть 17 квадратов больше половины квадрата.
Кроме того, посчитайте квадраты, покрытые частично меньше, чем наполовину, и каждый из них будет считаться равным 0.На 16 квадратов меньше половины квадрата.
Теперь сложите все квадраты, чтобы найти площадь листа = 64 + 17 x 1 + 16 x 0 = 64 + 17 = 81 кв. единиц.
Отсюда площадь листа будет 81 кв.
Площадь неправильных фигур Формула
Чтобы найти площадь неправильных фигур, сначала нам нужно разделить неправильную форму на правильные фигуры, которые вы можете распознать, такие как треугольники, прямоугольники, круги, квадраты и так далее.
Затем найдите площадь этих отдельных фигур и сложите их, чтобы получить площадь неправильной формы.
Пример решена
В. Найдите площадь данной фигуры?
Sol: На рисунке выше три правильные фигуры. Начинайте делить сверху, у него есть треугольник, прямоугольник и трапеция.
Мы найдем площадь каждой из этих трех фигур и суммируем результаты, чтобы получить окончательную площадь фигуры.
Треугольник
Площадь треугольника = (основание × высота)/2
= (3 × 4)/2
= 12/2
= 6
Прямоугольник
Площадь прямоугольника = длина 0 × ширина
= 3 × 10= 30
Трапеция
Площадь трапеции = ((b 1 + b 2 ) × h)/2
= ((3 + 5) × 3040/2 9 040 2)/2 9 040 = (8) × 2/2
= 16/2
= 8
Отсюда площадь данной формы = 6 + 30 + 8 = 44.
Неправильные четырехугольники | Площадь, определение и видео // Tutors.com
Содержание
Иногда жизнь проста и прямолинейна. Квадраты привычны и удобны, регулярны и предсказуемы. Прямоугольники, трапеции, воздушные змеи и другие необычные четырехугольники, напротив, не так просты. Для неправильных четырехугольников даже такая простая задача, как нахождение их площади, может оказаться сложной задачей.
- Четырехугольник Определение
- Правильные четырехугольники
- Неправильные четырехугольники
- Площадь неправильного четырехугольника
- Площадь очень неправильных четырехугольников
Четырехугольник Определение
Напомним, что четырехугольник (лат. «четыре стороны» ) — это двумерная плоская фигура, которая использует четыре отрезка, чтобы заключить пространство.Поскольку определение настолько широкое, многие распространенные формы являются четырехугольниками:
- Квадраты
- Прямоугольники
- Трапеции
- Параллелограммы
- Воздушные змеи
- Ромбы
Правильные четырехугольники
Из длинного списка только квадрат является правильным четырехугольником . Правильные многоугольники имеют равные стороны и углы. Легко видеть, что прямоугольник может иметь четыре внутренних угла по 90°, но не обязательно иметь четыре стороны одинаковой длины.
Правильные многоугольники имеют равные стороны и углы. Легко видеть, что прямоугольник может иметь четыре внутренних угла по 90°, но не обязательно иметь четыре стороны одинаковой длины.
Неправильные четырехугольники
Что такое неправильный четырехугольник ? К неправильным четырехугольникам относятся: прямоугольник, трапеция, параллелограмм, воздушный змей и ромб. Они симметричны, но не обязаны иметь конгруэнтные стороны или углы. Однако не отчаивайтесь, потому что некоторые из них, как и квадрат, поддаются формулам площади.
Кроме симметричных неправильных четырехугольников могут существовать и другие неправильные четырехугольники без симметрии, всего четыре неравные стороны:
[вставить чертеж неправильного четырехугольника MATH с обозначенными сторонами MA = 7 см, AT = 3 см, TH = 12 см, HM = 14 см]
Площадь неправильного четырехугольника
Вычислить площадь (в квадратных единицах) для квадрата и прямоугольника очень просто:
- A = Ширина x Длина (Ш x Д), что для квадрата означает то же самое, что и W^2.

Если у вас есть квадрат со стороной 17 см, площадь равна 289 квадратных см. Если у вас есть прямоугольник с двумя сторонами 17 см и двумя сторонами 34 см, площадь равна 17 х 34 = 578 квадратных см.
Вычисление площади для большинства других неправильных четырехугольников может оказаться сложной задачей. Площадь параллелограмма или ромба, например, равна его высоте (или высоте), а не длине его короткой стороны, умноженной на его основание. Для трапеции нужно найти среднее значение двух оснований и умножить его на высоту трапеции.
Воздушный змей , который имеет две смежные короткие стороны и две смежные длинные стороны, имеет формулу площади, основанную на его диагоналях, d1 и d2:
Площадь очень
Неправильных четырехугольниковНаш предыдущий пример неправильного четырехугольника, МАТЕМАТИКА, показывает, что четыре стороны не гарантируют симметричную форму. Чтобы найти площадь таких неправильных четырехугольников, следуйте трехэтапной стратегии:
- Разделите четырехугольник на два треугольника, построив диагональ, не нарушающую известный внутренний угол
- Рассчитайте площадь каждого треугольника по формуле
- Сложите площади двух треугольников
Для нашего четырехугольника MATH соединение вершины A с вершиной H разбивает форму на △MAH и △ATH. Вы не знаете высоты h обоих треугольников, поэтому вы не можете вычислить площадь, используя 1/2bh.
Вы не знаете высоты h обоих треугольников, поэтому вы не можете вычислить площадь, используя 1/2bh.
Вместо этого проявите немного творчества (математика полна творчества), строя один факт на другом. В нашем четырехугольнике МАТЕМАТИКА, если мы знаем один угол, мы можем использовать эти четыре шага, чтобы найти общую площадь:
- Зная, что угол T равен 120°, вы можете использовать функцию Сторона-Угол-Сторона, чтобы найти площадь △ATH
- Зная площадь △ATH, вы можете использовать закон косинусов для вычисления неизвестной длины диагонали AH
- Зная длину диагонали AH, вы можете использовать формулу Герона для вычисления площади △MAH
- Зная площади двух треугольников, сложите их, чтобы получить площадь неправильного четырехугольника
Обратите внимание, что вы должны работать последовательно, и для начала у вас должны быть некоторые основные факты.2 = 189
Теперь у нас есть приблизительная длина стороны AH, равная 13,747 см, поэтому мы можем использовать Формулу Герона для вычисления площади другой части нашего четырехугольника.
Использовать Формулу Герона
Формула Герона зависит от знания полупериметра или половины периметра треугольника. Для нашего △MAH три стороны:
- МА = 7 см
- АХ = 13,747 см
- НМ = 14 см
Полупериметр s , половина суммы сторон:
- с = ½(7 см + 13.2
С точностью до тысячных квадратных см мы имеем площадь четырехугольника МАТЕМАТИКА!
Краткое содержание урока
Теперь, когда вы полностью проработали урок, вы можете различать четырехугольники, различать правильные и неправильные четырехугольники, а также вспоминать и объяснять отличительные свойства правильных и неправильных четырехугольников. Теперь вы также можете применять длину на ширину в качестве формулы для вычисления площади правильных и некоторых неправильных четырехугольников, и, когда формула длины на ширину неприменима, находить площадь неправильных четырехугольников с помощью других стратегий, в том числе с использованием закона косинусов и формулы Герона.
Следующий урок:
Что такое четырехугольник?
Площадь неправильных многоугольников
Введение
Я просто решил поделиться с вами умной техникой, которую я когда-то использовал для нахождения площади обычных многоугольников.
Многоугольник может быть правильным (все углы равны и все стороны равны) или неправильным
| Обычный | Нестандартный |
Пример полигона
Возьмем в качестве примера этот многоугольник:
Координаты
Первый шаг — превратить каждую вершину (угол) в координату, как на графике:
Площадь под одним сегментом линии
Теперь для каждого отрезка вычислите площадь вниз по оси x .
Итак, как рассчитать каждую площадь?
Усреднить две высоты, затем умножить на ширину
Пример: Для фигуры, выделенной выше, мы берем две высоты (координаты «y» 2,28 и 4,71) и вычисляем среднюю высоту:
(2,28+4,71)/2 = 3,495
Вычислите ширину (разница между координатами «x» 2,66 и 0,72)
2,66-0,72 = 1,94
Площадь ширина×высота:
1. 94 × 3,495 = 6,7803
94 × 3,495 = 6,7803
Добавить их всех
Теперь сложите их все!
Но хитрость заключается в том, чтобы складывать, когда они идут вперед (положительная ширина), и вычитать, когда они идут назад (отрицательная ширина).
Если вы всегда ходите вокруг многоугольника по часовой стрелке и всегда вычитаете первую координату «x» из второй, это получается естественным образом, вот так:
| Из | — | |||||
|---|---|---|---|---|---|---|
| х | и | х | и | Средняя высота | Ширина (+/-) | Площадь (+/-) |
| 0.72 | 2,28 | 2,66 | 4,71 | 3,495 | 1,94 | 6.7803 |
| 2,66 | 4,71 | 5 | 3,5 | 4.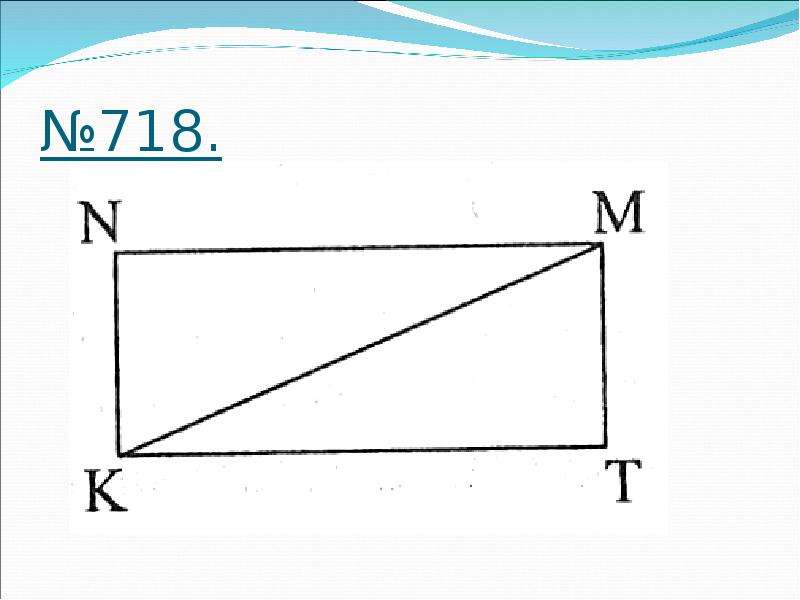 105 105 |
2,34 | 9.6057 |
| 5 | 3,5 | 3,63 | 2,52 | 3.01 | -1.37 | -4.1237 |
| 3,63 | 2,52 | 4 | 1,6 | 2,06 | 0,37 | 0,7622 |
| 4 | 1,6 | 1,9 | 1 | 1,3 | -2,1 | -2,7300 |
| 1,9 | 1 | 0,72 | 2.28 | 1,64 | -1,18 | -1,9352 |
| Всего: | 8.3593 | |||||
Вы также можете пойти в другом направлении. Если вы получили отрицательную область, просто сделайте ее положительной.
А выглядит это так:
Вот оно! Площадь 8. 3593
3593
Область инструмента «Многоугольник»
Рад, что вы дочитали до этого места! В награду вы получите ссылку на инструмент рисования области многоугольника, который может сделать все это за вас. Он также принимает ручной ввод координат.
Площадь любого неправильного четырехугольника
Плоская фигура, ограниченная четырьмя отрезками прямой, называется неправильным четырехугольником. Площадь любого неправильного четырехугольника можно вычислить, разделив его на треугольники.2}} = \sqrt {1681} = 41 \\ \end{собрано} \]
Теперь площадь $$\Delta ABD = \frac{1}{2} \times 40 \times 9 = 180$$ м
В $$\Delta BCD$$ $$BD = a = 41$$ m, $$DC = b = 28$$ m, $$CB = c = 15$$ m
$$\следовательно, s = \frac{{a + b + c}}{2} = \frac{{41 + 28 + 15} {2} = 42$$ м
Теперь,
\[\begin{gathered} {\text{Area}}\,{\text{of}}\,\Delta BCD = \sqrt {s(s – a)(s – b)(s – c)} \, \\ {\text{Площадь}}\,{\text{из}}\,\Delta BCD = \sqrt {42(42-41)(42-28)(42-15)} = \sqrt {42 \times 14 \times 27} = 126\,sq\,m \\ \end{собрано} \]
Площадь четырехугольника $$ABCD$$$$ = $$ площадь $$\Delta ABD$$ $$ + $$площадь $$\Delta BCD$$
Площадь четырехугольника $$ABCD$$ $$ = (180 + 126) = 306$$ квадратных метров.
Пример :
Диагональ четырехугольника равна $$42$$ см, а два перпендикуляра к нему из других вершин равны $$8$$ см и $$9$$ см соответственно. Найдите площадь четырехугольника.
Решение :
Учитывая, что из фигуры $$AC = 42$$ м, $$BN = 9$$ м, $$DM = 8$$ м
Площадь $$ABCD = $$ площади $$\Delta ABC + $$площадь $$\Delta ACD$$
Площадь $$ABCD$$$$ = \frac{1}{2} \times 9 \times 42 + \frac{1}{2} \times 8 \ умножить на 42 = 189 + 168 = 357$$ квадратных метров.
Площадь неправильных фигур
Может показаться, что найти площадь прямоугольника несложно, но что, если у фигуры больше четырех сторон?
Обратите внимание, что у этой фигуры 8 сторон. Поэтому мы могли бы назвать его восьмиугольником.
Однако заученная наизусть формула неправильного восьмиугольника не очень поможет в этой ситуации. Вместо этого разбейте фигуру на прямоугольники.
Затем вычислите площади обоих прямоугольников и сложите их вместе.
Площадь первого прямоугольника 72 квадратных сантиметра, площадь второго прямоугольника 50 квадратных сантиметров.
Вместе 72 + 50 = 122 квадратных сантиметра.
Следовательно, площадь всей фигуры равна 122 квадратных сантиметра.
Иногда проще всего сложить части. В других случаях вы можете использовать другой подход. Посмотрите следующий пример.
Обратите внимание, что эта фигура выглядит как квадрат, в котором отсутствует часть.
В этом случае вычислите площадь квадрата и прямоугольника, а затем вычтите.
квадрат = S 2 A = BH
A = (30 дюймов) 2 a = (18 дюймов) (10 дюймов)
a = 900 в. 2 a = 180 дюймов 2
Площадь синего шестиугольника составляет 900 дюймов 2 — 180 дюймов 2 = 720 дюймов 2 .
Путем сложения площадей или вычитания площадей прямоугольников можно вычислить площадь неправильной формы. Это не будет работать для всех неправильных фигур. Возможно, вам придется использовать треугольники или другие формы.
Это не будет работать для всех неправильных фигур. Возможно, вам придется использовать треугольники или другие формы.
Начните с того, что разбейте эту фигуру на прямоугольники и треугольники. Существует более одного правильного способа сделать это. Вот один из возможных вариантов:
Затем используйте известные длины сторон, чтобы определить любые длины сторон, которые все еще необходимы для вычисления площади трех частей.
Здесь мы добавили все части верхней длины. Затем мы можем вычесть это из 9 единиц, чтобы получить основание треугольника.
Теперь все основания и высоты помечены, чтобы можно было вычислить площади.
A Верхний прямоугольник = BH A Большой прямоугольник = BH A Треугольник = 1/2 BH
A = (3,5 единицы) (1,5 единицы) A = (5,5 единицы) (5,5 единицы) = 1/2 (3,5 ед.)(4 ед.)
A = 5,25 ед. 2 A = 30,25 ед. A = 30,25 ед. 25 единиц 2 + 30,25 единиц 2 + 7 единиц 2
25 единиц 2 + 30,25 единиц 2 + 7 единиц 2
Общая площадь = 42,5 единиц 2
Вот последний пример: . Поскольку мы удаляем прямоугольники, площадь меньших прямоугольников необходимо вычесть из общей площади треугольника.
A Треугольник = 1/2 BH A N Верхний прямоугольник = Bh A Нижний прямоугольник = BH
A = 1/2 (18 мм) (13 мм) A = (5 мм) (3 мм) a = (7 мм) (2 мм)
a = 117 мм 2 a = 15 мм 2 a = 14 мм 2 a = 14 мм 2
Следовательно, общая площадь оранжевых фигур:
117 мм 2 — 15 мм 2 — 14 мм 2 = 88 мм 2
Давайте рассмотрим Когда вас попросят определить площадь неправильной фигуры, вы можете попробовать два основных метода.Оба они включают в себя разбиение неправильных фигур на формы, с которыми вы можете работать.
 Для других четырёхугольников средние линии – отрезки.
Для других четырёхугольников средние линии – отрезки.