Что означает уклон в процентах, и как перевести его в градусы
Когда идет речь о кровле зданий, то под словом «уклон» подразумевают угол наклона оболочки крыши к горизонту. В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.
Расчет уклона в процентах
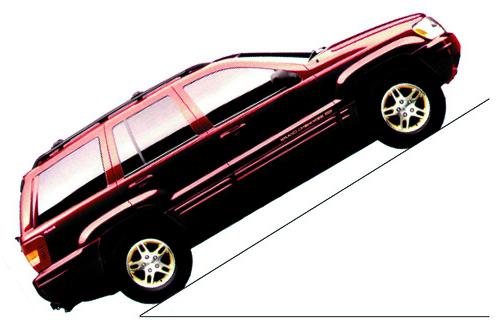
Попробуйте представить прямоугольный треугольник АВС, лежащей на одном из своих катетов АВ. Второй катет ВС будет направлен вертикально вверх, а гипотенуза АС образует с нижним катетом некий угол. Теперь нам предстоит немножко вспомнить тригонометрию и рассчитать его тангенс, который как раз и будет характеризовать уклон, образуемый гипотенузой треугольника с нижним катетом. Предположим, что катет АВ = 100 мм, а высота ВС = 36,4 мм. Тогда тангенс нашего угла будет равен 0,364, что по таблицам соответствует 20˚. Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.
Как понимать угол уклона в процентах?
Если дорожный знак показывает 12%, то это означает, что на каждом километре такого подъема или спуска дорога будет подыматься (опускаться) на 120 метров. Чтобы перевести процентное значение в градусы, нужно попросту вычислить арктангенс этого значения и при необходимости перевести его из радиан в привычные градусы. То же самое касается и строительных чертежей. Если, к примеру, указывается, что угол уклона в процентах равен 1, то это означает, что соотношение одного катета к другому равно 0,01.

Почему не в градусах?
Многих наверняка интересует вопрос: «Зачем для уклона использовать еще какие-то проценты?» Действительно, почему бы просто не обойтись одними градусами. Дело в том, что при любых измерениях всегда имеет место некоторая погрешность. Если в проектной документации станут применять градусы, то неминуемо возникнут сложности с монтажом. Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.
Применение на практике
Предположим, что проект строительства загородного дома предполагает устройство скатной кровли. Требуется проверить ее уклон в процентах и градусах, если известно, что высота конька составляет 3.45 метра, а ширина будущего жилища равна 10 метрам. Так как спереди крыша представляет собой равносторонний треугольник, то ее можно разделить на два прямоугольных треугольника, в которых высота конька будет являться одним из катетов. Второй катет находим, разделив ширину дома пополам.
 Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan-1(0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.
Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan-1(0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.Почему крутизна склонов измеряется в процентах, и зачем водителям это нужно
Наверняка вы уже ни раз встречали предупреждающие дорожные знаки 1.13, он же «Крутой спуск», и 1.14 (соответственно, «Крутой подъем»). И кто-то из водителей точно обратил внимание, что уклон обозначен не в привычных градусах, а в процентах. Градусы – они же и при температуре, и в спиртном. Родные, понятные. Зачем все усложнять? Настало время разобраться с этим недоразумением и узнать, как автомобилистам может помочь данная информация при езде.
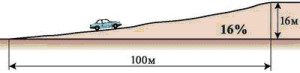
Представьте ситуацию: едете вы за городом и встречаете перед собой дорожный знак, предупреждающий водителей о том, что впереди подъем с крутизной уклона в 10%. Как на картинке выше. В голове сразу: 10% – это вообще сколько? Но если мы скажем, что это почти 6 градусов, вам разве станет от этого понятнее?
Тут важно понимать, что дорога постоянно меняет угол своего наклона, поэтому определить этот показатель в градусах будет сложновато. Зато уклон дороги в процентах – легко! Это то количество метров, на которое проезжая часть опустится или поднимется через 100 метров пути. То есть в нашем случае, проехав 1 километр по дороге с крутизной уклона в 10%, вы поднимитесь на 100 метров относительно первоначальной точки. Если вспоминать школьный курс тригонометрии, то цифра на дорожном знаке – это тангенс угла наклона проезжей части, выраженный в процентах. Впрочем, не заморачивайтесь: за вас уже давно все подсчитали, а вам нужно просто научиться этими данными пользоваться.
Зачем нужно знать крутизну склона?
Оказывается, тангенс угла наклона равняется коэффициенту сцепления с дорожным покрытием. Если вы едете по сухому асфальту, этот показатель составляет около 0,7 (при условии, что у вас не «лысая» резина). Пошел дождь – коэффициент сцепления с мокрой дорогой сразу упал до 0,5. А если дело происходит поздней осенью, и после ливня «удачно» подморозило, то асфальт превращается в настоящий каток. И тут уже коэффициент сцепления с проезжей частью снижается до минимума – менее 0,1. Что это значит в нашей ситуации, когда мы поднимаемся в горку с крутизной уклона в 10%, или 0,1?
Вы должны понимать, что, если вы остановитесь на склоне, то, в лучшем случае, не сможете тронуться, чтобы продолжить путь, в худшем – автомобиль с легкостью покатится обратно. И никакой водительский опыт или даже самая лучшая шипованная резина не помогут автомобилю остановиться, пока он не скатится с горы. Потому что с дорогой колеса практически ничего не связывает. Именно поэтому Правила дорожного движения (п. 11.7 ПДД) принуждают спускающихся со склона водителей уступать встречному поднимающемуся в гору потоку (даже, если препятствие расположено на их половине дороги).
Чем опасен затяжной спуск
Съезд с крутой горы – не менее опасное мероприятие. Во время длительного спуска, когда вы беспрерывно давите на педаль тормоза, в автомобиле могут перегреться и отказать тормоза. Чтобы этого не случилось, советуем научиться «гасить скорость» при помощи двигателя, постепенно снижая передачи. Чем круче спуск, тем ниже должна быть передача. Об особенностях торможения двигателем мы подробно писали в нашем блоге ранее.
Кстати, многие не обращают особого внимания на знаки «Крутой спуск» или «Крутой подъем». Особенно, когда там указан небольшой процент крутизны склона. Напрасно. Нередко случается, что в условиях плохой погоды (например, в снегопад, туман или когда темно) автомобилист может попросту не заметить небольшие, но затяжные спуски или подъемы. А именно на них чаще всего и перегреваются тормоза. Так что знаки не пропускаем. Стали бы чиновники тратить деньги из местного бюджета, если бы данный отрезок дороги не представлял никакой опасности?
Разница в знаках
Ну и напоследок расскажем о том, как отличить спуск и подъем на знаках. Конечно, чаще всего можно понять, что перед тобой чисто визуально. Но не всегда. Погода вносит коррективы, и в сильный снегопад небольшой длительный спуск можно запросто не заметить, а тормозная система автомобиля заметит. Так что в плохую погоду стоит особенно внимательно смотреть на знаки, установленные на обочине.
Отличить спуск от подъема на дорожных знаках вам поможет левая рука. Направьте ладонь по наклонной линии, над которой написана крутизна склона в процентах. Если пальцы будут направлены вниз, значит перед вами крутой спуск, если вверх, то значит вам предстоит забираться в гору.
К счастью, наибольшие продольные уклоны на автомобильных дорогах России не превышают 6-7% на равнинной и холмистой местности и 9-10% в горах. Конечно, в приморских городах есть дороги с довольно серьезными склонами, крутизна которых превышает все имеющиеся нормативы. Но мы-то теперь знаем, где опасность, а значит преодолеем даже самые крутые подъемы и спуски. Удачи на дорогах!
Поделитесь с друзьями
Подпишитесь на рассылку
таблица и расчет опт. и мин. угла
Строительство крыши –важный заключительный этап строительства дома. Крыша защищает дом от агрессивного воздействия окружающей среды, придает постройке эстетичный вид.
Плоски крыши преобладают в многоэтажных домах, в частных домах и коттеджах – скатные. Угол наклона крыши – важный расчетный показатель.
Виды крыш и их зависимость от угла наклона
Существует несколько видов крыш, в зависимости от устройства кровли:
- Односкатная крыша – наклонная плоскость, лежащая на стенах разной высоты.
- Двухскатная крыша – состоит из двух скатов, является надежной и простой.
- Вальмовая крыша – состоит из 4-х скатов со срезанными вершинами.
- Шатровое перекрытие – несколько равнобедренных треугольников, соединенных между собой вершинами.
Если угол наклона кровли более 10°, то крыша считается скатной.
От чего зависит уклон кровли
- от ветра
- от кровельного покрытия
- от архитектурных задумок
- от атмосферных осадков (снега и дождя)
Уклон крыши – это угол наклона кровли относительно горизонта.
Показатель уклона позволяет:
- Подобрать кровельный материал
- Правильно рассчитать количество снегодержателей
Зная одну из величин по таблице можно найти остальные значения.
Минимальный уклон для кровельных материалов (покрытий)
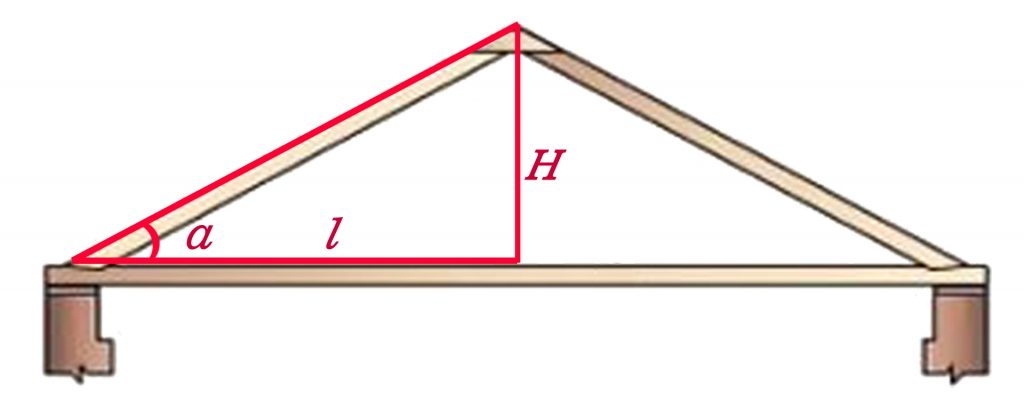
Пример №1.
H = 2 м
I = 2,86 м
Рассчитаем угол кровли (i): 2/2,86 = 0,699. Это 35° по данным таблицы.
Пример №2
Коэффициент уклона кровли 1,006. Найти: градус уклона кровли.
По таблице этому коэффициенту соответствует значение в 6° градусов.
Опубликовано в ИнформацияУклон. Угловые градусы — перевод в % уклона. Длина на метр (единицу) подьема. Таблица 0-90°
Уклон. Угловые градусы — перевод в % уклона. Длина на метр (единицу) подьема — градиент индикатор. Таблица 0-90°
- % уклон это 100 * Y/X (подъем / горизонтальная проекция длины)
| Угловые градусы | % уклона | ||
|---|---|---|---|
| Y | X | ||
| 0.1 | 1 | 573.0 | 0.17 |
| 0.2 | 1 | 286.5 | 0.35 |
| 0.3 | 1 | 191.0 | 0.52 |
| 0.4 | 1 | 143.2 | 0.70 |
| 0.5 | 1 | 114.6 | 0.87 |
| 0.57 | 1 | 100 | 1 |
| 0.6 | 1 | 95.49 | 1.05 |
| 0.7 | 1 | 1.22 | |
| 0.8 | 1 | 71.62 | 1.40 |
| 0.9 | 1 | 63.66 | 1.57 |
| 1 | 1 | 57.29 | 1.75 |
| 2 | 1 | 28.64 | 3.49 |
| 3 | 1 | 19.08 | 5.24 |
| 4 | 1 | 14.30 | 6.99 |
| 5 | 1 | 11.43 | 8.75 |
| 5.74 | 1 | 10 | 10 |
| 6 | 1 | 9.514 | 10.5 |
| 7 | 1 | 8.144 | 12.3 |
| 8 | 1 | 7.115 | 14.1 |
| 9 | 1 | 6.314 | 15.8 |
| 10 | 1 | 5.671 | 17.6 |
| 11 | 1 | 5.145 | 19.4 |
| 12 | 1 | 4.705 | 21.3 |
| 13 | 1 | 4.331 | 23.1 |
| 14 | 1 | 4.011 | 24.9 |
| 15 | 1 | 3.732 | 26.8 |
| 16 | 1 | 3.487 | 28.7 |
| 17 | 1 | 3.271 | 30.6 |
| 18 | 1 | 3.078 | 32.5 |
| 19 | 1 | 2.904 | 34.4 |
| 20 | 1 | 2.747 | 36.4 |
| 21 | 1 | 2.605 | 38.4 |
| 22 | 1 | 2.475 | 40.4 |
| 23 | 1 | 2.356 | 42.4 |
| 24 | 1 | 2.246 | 44.5 |
| 25 | 1 | 2.145 | 46.6 |
| 26 | 1 | 2.050 | 48.8 |
| 27 | 1 | 1.963 | 51.0 |
| 28 | 1 | 1.881 | 53.2 |
| 29 | 1 | 1.804 | 55.4 |
| 30 | 1 | 1.732 | 57.7 |
| 31 | 1 | 1.664 | 60.1 |
| 32 | 1 | 1.600 | 62.5 |
| 33 | 1 | 1.540 | 64.9 |
| 34 | 1 | 1.483 | 67.5 |
| 35 | 1 | 1.428 | 70.0 |
| 36 | 1 | 1.376 | 72.7 |
| 37 | 1 | 1.327 | 75.4 |
| 38 | 1 | 1.280 | 78.1 |
| 39 | 1 | 1.235 | 81.0 |
| 40 | 1 | 1.192 | 83.9 |
| 41 | 1 | 1.150 | 86.9 |
| 42 | 1 | 1.111 | 90.0 |
| 43 | 1 | 1.072 | 93.3 |
| 44 | 1 | 1.036 | 96.6 |
| 45 | 1 | 1.000 | 100.0 |
| 46 | 1 | 0.9657 | 103.6 |
| 47 | 1 | 0.9325 | 107.2 |
| 48 | 1 | 0.9004 | 111.1 |
| 49 | 1 | 0.8693 | 115.0 |
| 50 | 1 | 0.8391 | 119.2 |
| 51 | 1 | 0.8098 | 123.5 |
| 52 | 1 | 0.7813 | 128.0 |
| 53 | 1 | 0.7536 | 132.7 |
| 54 | 1 | 0.7265 | 137.6 |
| 55 | 1 | 0.7002 | 142.8 |
| 56 | 1 | 0.6745 | 148.3 |
| 57 | 1 | 0.6494 | 154.0 |
| 58 | 1 | 0.6249 | 160.0 |
| 59 | 1 | 0.6009 | 166.4 |
| 60 | 1 | 0.5774 | 173.2 |
| 61 | 1 | 0.5543 | 180.4 |
| 62 | 1 | ||
Уклоны. Теория — на уровне глаз — ЖЖ
Как было сказано ранее, по одному из определений уклон это тангенс угла. С большим интересом узнал, что он равен коэффициенту сцепления. Вот тут и начинает прояснятся тайный смысл предупреждающих дорожных знаков 1.13 и 1.14 (крутой спуск / подъём).
Коэффициентом сцепления называется отношение двух сил – силы, необходимой для сдвига машины с заблокированными колесами, и силы тяжести, прижимающей машину к дороге. Так мы легко можем получить коэффициенты сцепления для сухого асфальта – 7000/10000 = 0,7, для грязной дороги – 3000/10000 = 0,3, и для льда – 1000/10000 = 0,1.
Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой). Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. [2]
К тому же, «при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину. И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки 1.13 и 1.14. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае – не сможете сдвинуться с места. А уж если затормозите на спуске, машину может занести. Старайтесь тормозить двигателем на длительных спусках.» [2]
Вот о чём предупреждают знаки.
Кстати, есть знаки и меньше 10%, поэтому стало интересно в каких случаях их устанавливают.
ГОСТ Р 52289-2004 «Правила применения дорожных знаков, разметки, светофоров, дорожных ограждений и направляющих устройств», п. 5.2.16:
4% — если длина участка дороги на спуске или подъёме больше 600 метров при данном уклоне.
5% если больше 450 метров
6% если больше 350 метров
7% если больше 300 метров
8% (и более) если больше 270 метров.
Там же указаны и другие случаи, как например расстояние видимости, но сейчас они нас не интересуют.
Причины: почему проценты?
При рассмотрении темы уклонов всегда возникает вопрос, а почему уклон измеряют в процентах, а не в привычных градусах? По этому поводу слышал несколько версий:
а) КартыТак проще вычислять уклон рельефа на карте или на строительном плане. Рельеф на картах обозначается линиями — горизонталями. Это замкнутая линия, которая получается если мысленно сделать сечение на какой-либо высоте и посмотреть сверху. Проще это представить если вспомнить линию уреза воды реки или водоёма, это тоже своего рода горизонталь.
Горизонтали, т.е. горизонтальные сечения, проводятся через определённое постоянное расстояние по высоте, о чём указывается в примечаниях. Зная высоту сечения горизонталей и определив на карте расстояние между ними можно получить уклон. Чем ближе друг к другу на карте изображены горизонтали, тем рельеф круче.
б) Погрешность
Построить угол, заданный в градусах, так сказать «в натуре» на строительной площадке, задача не из простых, а построить точно и вовсе запредельная. Небольшие величины уклона в градусах имеют вид десятичных дробей, а ведь погрешность даже в 1° на 10 метров длины даст ошибочные 17 сантиметров высоты. Так же, проценты величина относительная, и потому уклон, выраженный в процентах, можно построить имея в распоряжении только рулетку (или иной инструмент для измерения длинны) и уровень.
в) Неравномерность
Дорога, на протяжении всего спуска (подъёма), имеет неравномерный уклон. В каждый отдельный момент угол разный, и поэтому проще посчитать сколько составляет горизонтальная длинна участка спуска (подъёма), и на сколько изменилась высота относительно начала спуска (подъёма).

seyfulmulyukov.livejournal.com / 1avtorul.ru
Все эти версии вполне имеют право на жизнь. Общим для них является то, что для нахождения величины уклона используются меры длинны, которые всегда есть под рукой, а это практично. Что касается дорожных знаков, то более правдоподобной выглядит третья версия (неравномерность уклона), а для строительства дорог вторая (погрешность построений).
Есть ещё Международная Конвенция о дорожных знаках и сигналах за 1968 год, и Европейское соглашение 1971 года, дополняющее эту Конвенцию, по которой на предупреждающих знаках крутизна уклонов и подъемов указывается в процентах. [3]
Что стоит за цифрами, например 1/12 или 10%, много это или мало, как это выглядит и где применяется, рассмотрим в следующий раз на примерах из жизни.
Использованные материалы
1. Словари и энциклопедии на Академике © Академик2. Материалы сайта «Школа жизни» © Shkolazhizni.ru
3. Википедия © Wikipedia
—
Уклоны. Практика — на уровне глаз — ЖЖ
Часть первая — теоретическая, в которой разбираем, что такое уклонЧасть вторая — техническая, про моделирование уклонов в 3D программах (ArchiCAD и SketchUp)
Часть третья — практическая, примеры из жизни
Время от времени приходится иметь дело с уклонами вообще, и пандусов в частности. «Один к шести», «один к двенадцати», десять процентов, восемь процентов и т.п. Что это? Теоретически это мы разобрали ранее, но хотелось бы знать, как это выглядит в натуре, чтобы понимать как будет «работать» то, что начертишь. В чём разница для «пользователя»? О чём говорят цифры: полого это или круто, удобно или неудобно, и насколько одно отличается от другого?
Пандусы
В СНиПе 31-06-2009 «Общественные здания и сооружения» (п. 5.6) по поводу уклонов пандусов говорится:
Уклон пандусов на путях передвижения людей не должен превышать:
внутри здания, сооружения — 1:6; снаружи — 1:8; на путях передвижения инвалидов на креслах-колясках, в том числе в стационарах лечебных учреждений — от 1:10 до 1:12.
На фото ниже представлены пандусы внутри здания с указанными уклонами — 1:6 и 1:12. Сразу видно, что 1/6 круче, чем 1/12. Заметно круче.
Посмотрели, теперь опишем физические ощущения от ходьбы по данным пандусам, и начнём с малого уклона.
1/12
Он же 8% (i=0,08), он же 4,8°. Это максимально допустимый уклон пандуса для инвалидов, согласно
СНиП 35-01-2001 «Доступность зданий и сооружений для маломобильных групп населения», раздел «Лестницы и пандусы»
п.3.29 Максимальная высота одного подъема (марша) пандуса не должна превышать 0,8 м при уклоне не более 8 %.
Стоит отметить, что там же, в разделе «Участки и территории» указана меньшая цифра:
3.3 Продольный уклон пути движения, по которому возможен проезд инвалидов на креслах-колясках, как правило, не должен превышать 5 %
То есть уклон вне зданий должен быть более пологим. Почему так? Условиями из пункта 3.29 вводятся ограничения в виде перепада высот (0,8 метра) и максимального уклона (8%). При данных условиях максимальная длинна горизонтальной проекции пандуса составит 9,6 метра. В п.3.3 таких ограничений нет, а значит длина может быть любой. Важно, что на удобство перемещения по наклонной плоскости влияет не только величина уклона, но и длинна наклонной поверхности. Поэтому, чем больше длина пандуса, тем меньше должен быть уклон. Даже крутой уклон, преодолеваемый за один шаг, может восприниматься легче, чем более пологий, но продолжительный. Дальнейшие примеры наглядно продемонстрируют, что такое 8% без ограничения длины. Мало не покажется.
Подъём
Переход от ровной поверхности к наклонной почти не заметен, но примерно на шестом шаге инерция горизонтального движения заканчивается, и начинает ощущаться лёгкий подъём.
Спуск
С первого шага отчётливо ощущается изменение характера поверхности (наклон плоскости). При каждом шаге чувствуется небольшой провал.
По ощущениям идти по нему не сложно, но шаг уже явно не такой как по ровной поверхности. Уже вполне отчётливо чувствуется уклон. Если он чувствуется для обычного пешехода, то думаю, что для человека на инвалидной коляске он ощутим очень даже. Подтверждением этого могут быть слова автора книги «Доступная среда глазами инвалида» Елены Геннадьевны Леонтьевой eleont:
Уклон поверхности до 5%, на мой взгляд, можно называть не пандусом, а просто изменением рельефа, выравниванием поверхности, пологим съездом, так как при таком уклоне инвалиду на коляске не требуется посторонняя помощь.
Уклон более 5% вызывает определенные трудности для инвалида на коляске, поэтому необходима установка поручней с двух сторон или помощь сопровождающего.
Архитекторы и проектировщики, имейте это в виду. Если есть возможность заложить в проект более пологий пандус – делайте обязательно. 1/16 (6%) – хорошо, 1/18 – замечательно, 1/20 (5%) – просто великолепно! Прислушайтесь к мнению людей в инвалидной коляске, и не дай нам Бог оказаться на их месте.
Интересно, что при уклоне 1/12 (8%) перепад высоты на один шаг (60 см) составляет 5 см. В нормах тоже фигурируют 5 см.[Нажмите, чтобы прочитать]
СНиП 31-06-2009 «Общественные здания и сооружения», п.5.9. В полу на путях движения не допускаются перепады высотой менее трех ступеней (при высоте ступеней не менее 0,12 м) и пороги выше 0,05 м.
или
СНиП 2.07.01-89* «Градостроительство. Планировка и застройка городских и сельских поселений», п.6.24. В селитебных районах, в местах размещения домов для престарелых и инвалидов, учреждений здравоохранения и других учреждений массового посещения населением следует предусматривать пешеходные пути с возможностью проезда механических инвалидных колясок. При этом высота вертикальных препятствий (бортовые камни, поребрики) на пути следования не должна превышать 5 см; не допускаются крутые (более 100‰) короткие рампы, а также продольные уклоны тротуаров и пешеходных дорог более 50‰. На путях с уклонами 30 — 60‰ необходимо не реже чем через 100 м устраивать горизонтальные участки длиной не менее 5 м.
По моим наблюдениям перепады высотой до 4 см при движении практически не замечаются. А вот 5 см это та крайняя высота, которая уже слабо, но ощущается как препятствие. Его еще явно не переступаешь, но уже нога движется иначе. Колено приподнимается чуть выше, чем при ходьбе по ровной поверхности, и стопа как бы переносится над препятствием.
Почему это так, в какой-то мере можно объяснить тем, что «центр тяжести тела во время Х. совершает движения во всех трёх плоскостях. По вертикали амплитуда его перемещений достигает 4—5 см»— М.: Советская энциклопедия 1969—1978
В связи с этим любопытным представляется, что СНиП 35-01-2001 «Доступность зданий и сооружений для маломобильных групп населения» требует в местах пересечения тротуаров с проезжей частью высоту не более 4 см.
3.4 Высота бортового камня в местах пересечения тротуаров с проезжей частью, а также перепад высот бордюров, бортовых камней вдоль эксплуатируемых газонов и озелененных площадок, примыкающих к путям пешеходного движения, не должны превышать 0,04 м.
Скорее всего, что в данном случае такая цифра вытекает из возможности колеса коляски преодолевать такие перепады высот, а не из-за особенностей ходьбы пешеходов. Хотя Елена Геннадьевна, в своей книге, даёт такой комментарий по этому поводу:
В России почему-то считается, что все инвалиды без исключения могут без проблем преодолеть перепад в 4 см. На самом деле это не так. В международной практике максимально допустимая высота перепада уровней составляет не более 1,3–1,5 см.
Леонтьева Е.Г. Доступная среда глазами инвалида: научно-популярное издание. – Екатеринбург: «БАСКО», 2001. – с.37.
Тем не менее такая норма на руку и пешеходам, так как обеспечивает для них постоянство ритма ходьбы, а значит и её удобство и комфорт.
1/6
Он же 17% (i=0,17), он же 9,5°. Это предельный, максимально допустимый, уклон пандуса для передвижения людей внутри здания, согласно
СНиП 31-06-2009 «Общественные здания и сооружения» п.5.6, который уже воспринимается «горкой». Круче делать нельзя.
Подъём
С первого шага ритм и характер ходьбы меняется — скорее поднимаешься, чем идёшь вперёд. Скорость заметно падает. Шаг короче обычного, тело наклоняется вперёд, чувствуются усилия толчковой ноги. Для придания телу дополнительной динамики в работу включаются руки. Идти по нему не легко, есть ощущение, что по лестнице перемещаться легче. Может быть просто это связано с непривычностью движений, а не с количеством прилагаемых усилий.
Спуск
Чувствуется «тянущая» вперёд сила, для противодействия которой корпус тела отклоняется назад. При каждом шаге но́ги пружинят, и прилагаются усилия для гашения силы ускорения. Иначе шаг легко может перейти в бег.
Дороги
Выше был показан уклон 8% (1/12). Но это было внутри здания, а теперь рассмотрим его снаружи.
Подходящие параметры есть у дороги и тротуаров по пр.Ватутина (от ул.Костюкова до ул.5 Августа), где на перекрёстке пр.Ватутина-ул.Костюкова, в направлении центра города, установлен знак 1.13 «Крутой спуск» с указаным уклоном 9%.
Думаю, что те, кто тут проходил или проезжал уклон этот маленьким не назовут
Как известно, знак указывает лишь угол между началом и концом участка дороги, а в этом промежутке, в каждый отдельный момент, угол может быть разным. Что и показали натурные замеры. Уклон 9% соответствует лишь участку дороги от перекрёстка пр.Ватутина-ул.5 Августа до пешеходного моста. Дальше, до пересечения с ул.Костюкова, уклон равен 8%.
Длина участка с уклоном 8-9% около 250 метров. Не всякий велосипедист осиливает такой подъём, многие идут пешком.
8% Спуск и подъём
Спуск не вызывает особых трудностей, а ощущения при ходьбе были описаны выше. Длительный же подъём, при таком уклоне, даётся не легко. Во время подъёма чувствуется как переставляются ноги, примерно так же, как по лестнице. Обращаешь на это внимание. Мышцы спины начинают выделять тепло. К концу подъёма наблюдается учащённое сердцебиение, увеличивается глубина дыхания и ощущается напряжение мышц ног, в особенности икр.
Если продолжить идти по пр.Ватутина в сторону центра, то на пути встретятся участки с уклонами 5, 7 и 4%
7%
Близко по ощущениям к 8%, но немного легче. Ещё нет глубокого дыхания, учащённого сердцебиения и взмокшей спины. Лёгкий вариант 8%.
5%
Спуск лёгкий, но перемещение уже не совсем «свободное», как при ходьбе по ровной поверхности.
При подъёме чувствуется слабое, еле заметное, приложение усилий, преодоление. Дыхание держится в «нормальном» режиме.
Выводы
Уклон поверхности до 4% включительно не имеет каких-либо существенных различий с ходьбой по горизонтальной поверхности. 5% представляется граничным значением, при котором уже начинают появляться лёгкие изменения в характере ходьбы. Ещё двигаешься без затруднений, но уже различается наклон поверхности. Уклоны больше 5% меняют режим ходьбы, и чем больше уклон, тем изменения заметнее. От величины уклона поверхности зависит расстояние, которое можно пройти без утомления. Чем больше уклон, тем меньше расстояние. Например, при уклоне 2% пройти 1-2 километра не составит труда, а если уклон 8%, то можно запыхаться уже на 150 метрах (при подъёме).
Для объяснения этого можно вспомнить то, что удалось найти по механике ходьбы. Для демонстрации движения человека по наклонной плоскости, я использовал картинку из статьи Адама Саммерса (Adam Summers) «The Biomechanist Went Over the Mountain», размещённой на сайте Natural History Magazine. Повторю её тут.
Данные и картинка © Natural History Magazine
На ней показана последовательность движений человека при ходьбе по ровной поверхности (1), с уклоном 5°(~8%) (2) и уклоном 15°(~26%) (3). Белыми точками обозначено положение общего центра масс (ОЦМ) тела человека, который при ходьбе действует как груз на конце перевёрнутого маятника. Амплитуда перемещений ОЦМ по вертикали составляет 4-5 см, при этом бо́льшая часть энергии (около 65%), затраченной на изменение высоты ОЦМ, сохраняется. Ходьба по плоскости с небольшим уклоном увеличивает затраты энергии на работу маятника, и амплитуду перемещений ОЦМ (2). Часть энергии расходуется на тепло, выделяемое мышцами, а часть всё ещё остаётся для последующих шагов. Но когда уклон становится больше (3), то уже вся энергия тратится на один шаг (так же, как и при восхождении по лестнице).
Отсюда можно вывести ориентировочную классификацию уклонов для пешеходной ходьбы на большие расстояния:
• идеальный 0-2%
• нормальный 2-4%
• допустимый 5-6%
• предельный 7-8%
всё что сверх 8% можно считать затруднительным с различной степенью тяжести.
Таким образом, судя по мои субъективные впечатлениям, увеличение затрат энергии на работу маятника начинается с уклона 5%.
Разница между уклонами в 2% ощущается и различается кинестетически (т.е. суставами и мускулами в движении).
При больших отрезках одного уклона изменения даже в 1% могут быть визуально заметны.
[Инструмент]
Инструмент
Для измерения уклонов использовал самостоятельно изготовленный прибор простой конструкции. Деревянная рейка длиной 1,10 метра (уж какая была), к которой прикреплён плотный картон (3 мм). На нём лист со шкалой и стрелка с грузиком. Можно в качестве стрелки использовать грузик подвешеный на нитке, но в таком случае придётся дольше ждать прекращеня колебаний.
шкала уклономера в процентах pdf, svg
Есть и второй, более современный и компактный, вариант — с помощью приложения Smart Protractor.
У него в настройках можно выставить показ измерений в радианах, градусах или процентах.
Неплохое приложение, но при измерении малых уклонов, из-за небольшой длины смартфона, точность может быть ±1%, а это многовато. В общем, использовать можно, но для качественного измерения нужно вначале точно откалибровать, а потом желательно сделать несколько замеров и сравнить их с показаниями механического уклономера. Это для понимания условий точного измерения (как держать смартфон, на что ставить, и т.п.)
На этом трилогия «Уклоны» завершена
до этого были:
Часть первая — теоретическая, в которой разбираем, что такое уклон
Часть вторая — техническая, про моделирование уклонов в 3D программах (ArchiCAD и SketchUp)
Напоследок скажу, что всё что описано выше не более чем личные впечатления. Мне это нужно, чтобы в процессе проектирования не только опираться на цифры из нормативных документов, но и иметь кинестетическое представление о них. Также буду признателен, если поделитесь своими впечатлениями, наблюдениями или дополнениями.
© Gre-kow, 2015. gre-kow.livejournal.com
При копировании активная ссылка http://gre-kow.livejournal.com/26916.html обязательна
«Как на плоской кровле формируют уклон?» – Яндекс.Кью
Чтобы понять, что лучше, металлочерепица или мягкая кровля, надо разобраться, для какой крыши подбирается материал и какие из характеристики интересуют вас больше всего. Оба материала долговечны и надежны, но имеют ряд различий.
1. Вес, толщина.
Металлочерепица – 4,5-6,5 кг/м2, битумная кровля – 7,5-15 кг/м2. Вес зависит от толщины и у металлочерепицы не превышает 0,55 мм, а у мягкой кровли доходит до 5 мм. Кроме того, надо учитывать, что второй материал нельзя монтировать на шаговую обрешетку и требует сплошного покрытия, а это увеличивает вес кровельного пирога.
2. Долговечность.
У обоих материалов практически одинаковый срок эксплуатации. Производители гарантируют 30-50 лет использования, в действительности он может доходить и до 70 лет.
3. Особенности монтажа.
Металлочерепицу укладывают на обрешетку с шагом, его подбирают в зависимости от ширины волны (60-80 см). Битумную черепицу монтируют только на плоское основание (необходима основа для приклеивания), поэтому перед укладкой потребуется обшить крышу плитами OSB или водостойкой фанерой.
Мягкую кровлю нельзя укладывать при отрицательной температуре и во время жары – в первом случае он становится хрупкой и ломается, во втором — размягчается и не выдерживает лишнего веса. У металлочерепицы таких ограничений нет.
4. Функциональность.
-Металлочерепица абсолютно устойчива к воздействию огня.
-Мягкая кровля считается пожаробезопасной, но плавится при контакте с прямым огнем, т.к. содержит горючие материалы.
-Плитки мягкой черепицы снижают шум дождя.
-Металлочерепица более «шумная», но если кровля тёплая, то утеплитель значительно снижает шум дождя.
5. Цена
Металлочерепица стоит в 1,5-2 раза меньше, чем мягкая кровля. Кроме того, у мягкой кровли есть расходы на укладку основания и оплату работы по монтажу – самому правильно уложить каждую плитку очень сложно.
Как можно увидеть, практически по всем параметрам выигрывает металлочерепица, поэтому ответ на вопрос: что лучше, металлочерепица или мягкая кровля, очевиден.
Можно подумать, что количество металлочерепицы сложно рассчитать, но это не так. Воспользуйтесь онлайн-калькулятором по расчёту металлочерепицы и убедитесь сами.
Уклон прямой
Purplemath
Одно из самых важных свойств прямой — это угол от горизонтали. Эта концепция отражена в так называемом «наклоне» линии.
Давайте посмотрим на прямую y = ( 2 / 3 ) x — 4.Его график выглядит так:
MathHelp.com
Чтобы найти наклон, нам понадобятся две точки от прямой.
Я выберу два значения x , вставлю их в линейное уравнение и решу для каждого соответствующего значения y . Если, скажем, я выберу x = 3, тогда:
Теперь предположим, что я выбрал x = 9; затем:
(Между прочим, я выбрал эти два значения x именно потому, что они были кратны трем; таким образом я знал, что смогу очистить знаменатель дроби, так что в итоге у меня получится хороший, аккуратные целые числа для моих результирующих значений и .Это не правило, что вы должны это делать, но это полезный метод.)
Итак, две найденные мной точки (3, –2) и (9, 2) находятся на прямой y = ( 2 / 3 ) x — 4.
Чтобы найти уклон, обозначенный как « м », мы можем использовать следующую формулу:
(Почему « м » вместо «уклон», а не, скажем, « с »? Официальный ответ: никто не знает.)
В случае, если вы раньше не сталкивались с номерами переменных, меньшими, чем заданные, они называются «индексами». Нижние индексы обычно используются для различения похожих вещей или, например, для отсчета в последовательностях. В случае формулы наклона нижние индексы просто указывают на то, что у нас есть «первая» точка (координаты которой обозначены индексом «1») и «вторая» точка (координаты которой отмечены индексом «2»). Другими словами, нижние индексы означают не что иное, как тот факт, что у нас есть две точки, с которыми мы работаем.
(Вам решать, какую точку обозначить как «первую», а какую — как «вторую». Как подсказывает логика, угол линии не изменится только потому, что вы посмотрели на две точки в в другом порядке.)
Для вычисления уклонов по формуле наклона важно, чтобы мы вычитали x и y в том же порядке . Для наших двух точек, если мы выберем (3, –2) в качестве нашей «первой» точки, то получим следующее:
Первое значение y выше, –2, было взято из точки (3, –2); второе значение y , 2, пришло из точки (9, 2); x -значения 3 и 9 были взяты из двух точек в том же порядке .
Если бы, с другой стороны, мы взяли координаты точек в обратном порядке, результат был бы точно таким же:
Как видите, порядок, в котором вы указываете точки, на самом деле не имеет значения, если вы вычитаете значения x в том же порядке, в котором вы вычитали значения y . Из-за этого формулу наклона можно записать, как это было выше, или, альтернативно, ее также можно записать как:
Позвольте мне подчеркнуть этот момент:
Не имеет значения, какую из двух формул «наклона» вы используете, и неважно, какую точку вы выберете в качестве «первой», а какую — «второй».Значение только имеет значение, так это то, что вы вычитаете свои x -значения в том же порядке , в котором вы вычитали свои y -значения.
Для тех, кому интересно, эквивалентность двух приведенных выше формул наклона может быть доказана, если отметить следующее:
y 1 — y 2 = y 1 + (- y 2 )
= — л 2 + л 1
= — л 1 — (- л 2 )
= — ( y 2 — y 1 )
Аналогично:
x 1 — x 2 = x 1 + (- x 2 )
= — x 2 + x 1
= — x 1 — (- x 2 )
= — ( x 2 — x 1 )
Затем первая формула преобразуется во вторую следующим образом:
м = ( y 1 — y 2 ) / ( x 1 — x 2 ) = [- ( y 2 — y 1 )] / [- ( x 2 — x 1 )] = ( y 2 — y 1 ) / ( x 2 — х 1 )
Как вы можете видеть выше, выполнение вычитания в так называемом «неправильном» порядке служит только для создания двух знаков «минус», которые затем отменяются.Результат: не беспокойтесь слишком сильно о том, какая точка является «первой», потому что это действительно не имеет значения. (И, пожалуйста, не присылайте мне электронное письмо, в котором утверждается, что порядок каким-то образом имеет значение или что одна из двух приведенных выше формул почему-то «неправильная». Если вы думаете, что я ошибаюсь, вставьте пары точек в обе формулы и попытайтесь доказать, что я ошибаюсь! И продолжайте подключать, пока не «увидите», что математика на самом деле верна.)
Вернемся к строке y = ( 2 / 3 ) x — 4 и найдем для нее еще несколько точек.Если я положу x = –3, тогда:
Если я позволю x = 0, то:
Это дает мне две точки: (–3, –6) и (0, –4). Если я нанесу эти две точки на линию, я получу две синие точки, показанные ниже:
Если я поднимусь по лестнице от первой точки ко второй (когда я двигаюсь вправо по оси x ), я получаю следующее:
Следующая точка, которую я использую, — (3, –2).Обозначив точку и нарисовав ступеньку, я получу:
А теперь внимательно посмотрите на эти ступеньки. Подсчитайте их по сетке, видимой на заднем плане. Вы увидите, что при переходе от одной точки на графике к другой я продвигался на два шага вверх и на три шага вперед. В терминах, привычных для строительной отрасли, эти ступеньки имеют (вертикальный) «подъем», равный 2, и (горизонтальный) «подъем», равный 3. Когда люди говорят о «уклоне» как о «подъеме через спуск», это что они имеют в виду.(Для получения дополнительной информации попробуйте здесь.)
Давайте найдем наклон другого линейного уравнения:
-
Найдите наклон y = –2 x + 3
На графике линия выглядит так:
Я выберу пару значений для x и найду соответствующие значения для y .Выбирая x = –1, я получаю:
y = –2 (–1) + 3 = 2 + 3 = 5
Выбирая x = 2, получаю:
y = –2 (2) + 3 = –4 + 3 = –1
Тогда точки (–1, 5) и (2, –1) находятся на прямой y = –2 x + 3. Затем наклон линии вычисляется как:
Между прочим, если вы посмотрите на график и начнете с любой точки на линии (для простоты выберите ту, которая также лежит на сетке), вы заметите, что ступенька идет вниз.Вы спускаетесь на два, на один; вниз два, больше одного; вниз два, больше одного. И это соответствует наклону, который мы нашли выше:
(два меньше) / (больше одного) = (–2) / (1) = –2
-
Найдите наклон прямой, проходящей через точки (–3, 5) и (4, –1).
В данном случае мне не нужно искать очки, потому что они уже мне их дали.Итак, я сразу перейду к формуле:
м = (5 — (–1)) / (- 3 — 4)
= (5 + 1) / (- 3 + (–4)) = (6) / (- 7)
= — (6/7)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске уклона по паре точек.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Нажав «Нажмите, чтобы просмотреть шаги», вы перейдете прямо на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)
URL: https: // www.purplemath.com/modules/slope.htm
,Уклон (градиент) прямой
Наклон (также называемый градиентом) прямой линии показывает, насколько крута прямая линия.
Рассчитать
Для расчета уклона:
Разделите изменение высоты на изменение горизонтального расстояния
| Наклон = Изменение Y Изменение X |
Поиграйте (перетащите точки):
Примеры:
|
Наклон этой прямой = 3 3 = 1 Таким образом, наклон равен 1 |
|
Наклон этой прямой = 4 2 = 2 |
||
| Линия круче, а значит, и уклон больше. | ||
|
Наклон этой прямой = 3 5 = 0,6 |
||
| Линия менее крутая, поэтому уклон меньше. | ||
Положительный или отрицательный?
Двигаясь слева направо, велосипедист должен пройти P на выезде P Угол наклона:
При измерении линии:
- Начиная слева и переходя через вправо,
положительный (но переход влево отрицательный). - Вверх положительный , а вниз отрицательный
|
Наклон = −4 2 = −2 |
Эта линия идет на вниз на по мере вашего движения, поэтому угол наклона у нее отрицательный.
Прямо через
|
Наклон = 0 5 = 0 |
Прямая (горизонтальная) линия имеет нулевой наклон.
Прямо вверх и вниз
|
Наклон = 3 0 = undefined |
Последний вариант немного сложнее… вы не можете делить на ноль,
, поэтому наклон прямой вверх и вниз (вертикальной) линии равен «undefined».
Взлетай и беги
Иногда горизонтальное изменение называется «бегом», а вертикальное изменение — «подъемом» или «падением»:
Это просто разные слова, никакие вычисления не меняются.
,
Наклон, градиент и пересечение уклона
Понятие наклона используется в различных разделах математики и работает с довольно часто, когда решение и построение графиков линейных уравнений. Наклон или степень наклона Линия определяется как степень крутизны или наклона линии.
В более математических терминах, учитывая плоскость, содержащую как ось x, так и ось y, Наклон можно определить как изменение координаты y, деленное на изменение координаты x.Уклон обычно обозначают
м.
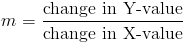
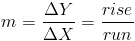
где символ Δ означает изменение на . Изменение y — это расстояние между обоими значениями y, что также называется подъемом . Изменение x равно расстояние между обоими значениями x, которое также называется пробегом . Склон также известен как рост над пробегом .
Учитывая две точки (X1, Y1) и (X2, Y2)

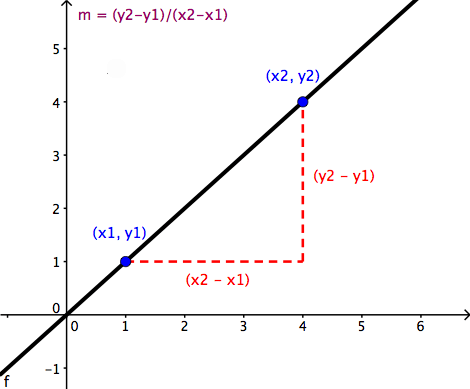
что совпадает с
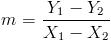
Хотя не имеет значения, с какой точки вы начнете, последовательность является обязательной. Ниже это пример НЕПРАВИЛЬНОГО способа вычисления уклона
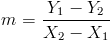
любая точка, выбранная вами в качестве начальной в числителе, ДОЛЖНА быть той же самой укажите в знаменателе
Наклон может быть положительным, отрицательным или нулевым:
- Положительный наклон означает, что линия увеличивается, другими словами движется слева направо.
- Отрицательный наклон означает, что линия уменьшается или перемещается справа налево.
- С другой стороны, нулевой наклон означает, что линия горизонтальна i.е. параллельно ось абсцисс.
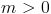
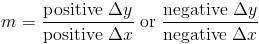
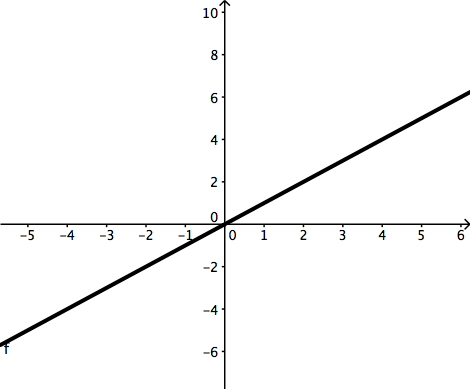

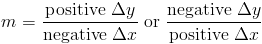

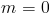
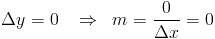
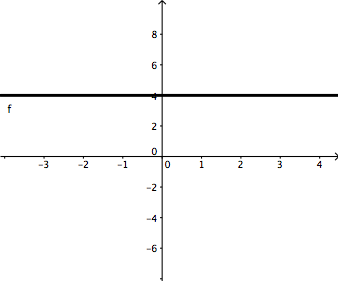
В некоторых случаях наклон может быть бесконечным или неопределенным, и это означает, что линия вертикально, т.е. параллельно оси y. Это происходит, когда нет изменений в ось x, т.е. (X1 — X2 = 0)
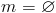
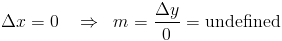
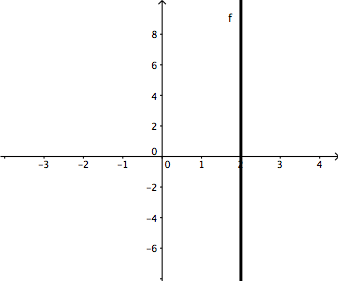
Величина наклона показывает крутизну линии; чем больше величина линии тем круче.
Форма пересечения склонов
Для прямой линии с пересечением наклона линии y = mx + b , где м представляет собой уклон, а b — постоянная величина, которая также называется Y-пересечение. Y-точка пересечения определяется как точка на оси Y, в которой линия (уравнение которой дано) пересекает ось y.
Имея в виду, что в любой точке оси Y координата x равна нулю (x = 0), простой способ получить точку пересечения по оси Y из уравнения прямой y = mx + b было бы просто установить x = 0 так, чтобы y = b.
Для данной прямой линии наклон постоянен, поэтому она не будет независимо от того, какие точки на линии вы выберете для расчета наклона.
Градиент в геометрии
В геометрии, учитывая линию который составляет угол θ с осью x, наклон m определяется как
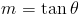
В геометрии градиенты линий можно использовать для определения их взаимосвязи. я.е. ли линии параллельно друг другу или перпендикуляр. Например: даны две линии с уклоном m1 и m2
.- Две прямые параллельны тогда и только тогда, когда их наклоны равны (т.е. m1 = m2) и
они не совпадают (т.е.не лежат друг на друге) или если они оба
вертикальные и поэтому имеют неопределенные уклоны (т. е. m1 = ∞ и m2 = ∞
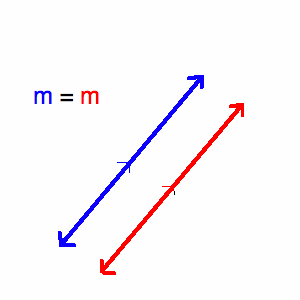
- Две линии перпендикулярны, если произведение их уклонов равно -1 (т.е.е. m1 x
m2 = -1) или один имеет наклон 0 (горизонтальная линия), а другой — неопределенный
наклон (вертикальная линия), т.е. m1 = 0 и m2 = ∞ или m1 = ∞ и m2 = 0.
Из вышесказанного обратите внимание, что с учетом двух перпендикулярных линий и наклона одной линии, вы всегда можете найти другой наклон из отношения

я.е.
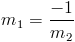
Наклон в исчислении
Исчисление в основном занимается кривые, уклоны / градиенты которых может быть труднее вычислить с использованием алгебраического метода. При работе с кривыми градиент меняется от точки к точке, поэтому мы можем только определить его в одной точке. Градиент в этой точке определяется как градиент касательной к этой точке. Касательная линия определяется как линия к кривой это касается только одной точки на кривой.2
Градиент в данной точке, скажем (1,1), находится путем взятия производной от уравнение, а затем подставив точку, т.е.
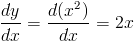
уклон м при (1,1)

Примеры уклона / градиента
(1) Найдите наклон линии между точками (1,2) и (3,6) .
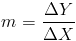
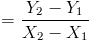
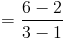
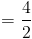
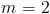
(2) Найдите наклон прямой 3y = 2x + 1
Это уравнение не имеет формы пересечения наклона, поэтому мы разделим на три, чтобы найти м значение.
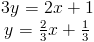

(3) Найдите наклон прямой 30 — 2y = -0.5x
Выделите y, чтобы преобразовать уравнение в форму пересечения наклона.
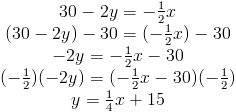
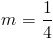
(4) Найдите градиент данной прямой y = mx + 3 в точке (2,5)
замените x и y
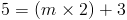
так что
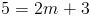
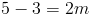
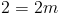
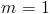
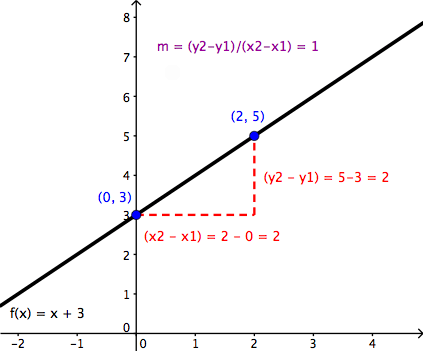
Как найти градусы прямой с учетом ее наклона?
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
математический
- Алгебра
- Исчисление
- Геометрия
- Prealgebra